如图，在平面直角坐标系中，有一Rt△ABC，且A(－1，3)，B(－3，－1)，C(－3，3)，已知△A1AC1是由△ABC旋转得到的． 请写出旋转中心的坐标是 ，旋转角是 度；
以(1)中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°、180°的三角形；
设Rt△ABC两直角边BC＝a、AC＝b、斜边AB＝c，利用变换前后所形成的图案证明勾股定理．
(本题满分10分)
已知：等腰三角形OAB在直角坐标系中的位置如图，点A的坐标为（
），点B的坐标为（－6，0）.
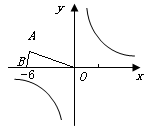
（1）若△OAB关于y轴的轴对称图形是三角形O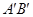
，请直接写出A、B的对称点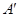
的坐标；
（2）若将△
沿x轴向右平移a个单位，此时点A恰好落在反比例函数
的图像上，求a的值．
(本题满分8分)
某隧道横断面由抛物线与矩形的三边组成，尺寸如图所示，某卡车空车时能通过此隧道，现装载一集装箱箱宽3
，车与箱共高4.5，此车能否通过此隧道？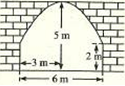
(本题满分8分)
已知扇形的圆心角为1200，面积为300πcm2.
（1）求扇形的弧长；
（2）若把此扇形卷成一个圆锥，则这个圆锥的轴截面面积是多少？
一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系：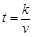
，其图象为如图所示的一段曲线，且端点为
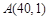和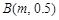
．
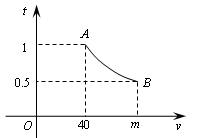
（1）求k和m的值；
（2）若行驶速度不得超过60（km/h），则汽车通过该路段最少需
要多少时间？
(本题12分)已知二次函数的图象如图所示．
（1）求二次函数的解析式及抛物线顶点M的坐标；
（2）若点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为s，求s与t之间的函数关系式及自变量t的取值范围；
（3）在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由；
（4）将△OAC补成矩形，使上△OAC的两个顶点成为矩形一边的两个顶点，第三个顶点落在矩形这一边的对边上，试直接写出矩形的未知的顶点坐标（不需要计算过程）．