(本小题12分)已知函数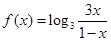 .
.
(1)证明函数 的图像关于点
的图像关于点 对称;
对称;
(2)若 ,求
,求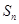 ;
;
(3)在(2)的条件下,若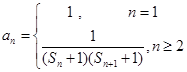
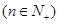 ,
, 为数列
为数列 的前
的前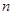 项和,若
项和,若 对一切
对一切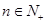 都成立,试求实数
都成立,试求实数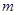 的取值范围.
的取值范围.
(本大题满分12分)在△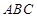 中,
中,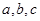 分别为内角
分别为内角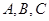 的对边,且
的对边,且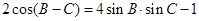
(1)求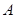
(2)若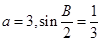 ,求
,求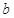
(本大题满分12分)已知点
(1)若 ,求
,求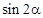 的值;
的值;
(2)若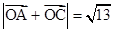 ,其中
,其中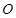 是原点,且
是原点,且 ,求
,求 与
与 的夹角。
的夹角。
(本小题满分14分)
函数 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)解不等式
(本小题满分14分)
设x,y,z∈R+,且3x=4y=6z.
(1)求证: ;(2)比较3x,4y,6z的大小.
;(2)比较3x,4y,6z的大小.
(本小题满分14分)
如图中,是一个长方体截去一个角所得多面体的直观图.它的正视图和侧视图在右面画出(单位:cm).
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥面EFG.