如图，是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减少传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB长为4米.求新传送带AC的长度(结果精确到0.1米)；
求新传送带与旧传送带货物着地点C、B之间的距离．(结果精确到0.1米，参考数据：
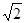≈1.41，
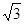≈1.73，
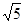≈2.24，
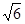≈2.45)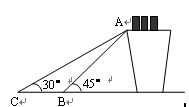
若关于x的方程2x-3=1和
=k-3x有相同的解，求k的值．
解方程：
－
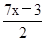＝1
解方程：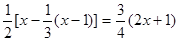
在平面直角坐标系内，已知点A(0，6)、点B(8，0)，动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．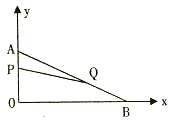
(1)求直线AB的解析式；
(2)当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时，求四边形OPQB的面积．
统计2010年上海世博会前20天的日参观人数，得到如下频数分布表和频数分布直方图(部分未完成)：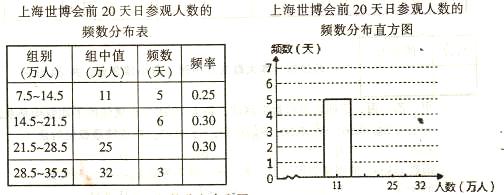
(1)请补全频数分布表和频数分布直方图；
(2)求出日参观人数不低于22万的天数和所占的百分比；
(3)利用以上信息，试估计上海世博会(会期184天)的参观总人数．