如图所示，直角坐标系xoy位于竖直平面内，在‑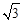
m≤x≤0的区域内有磁感应强度大小B = 4．0×10-4T、方向垂直于纸面向里的条形匀强磁场，其左边界与x轴交于P点；在x＞0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的有界匀强电场，其宽度d = 2m。一质量m = 6．4×10-27kg、电荷量q =-3．2×10‑19C的带电粒子从P点以速度v = 4×104m/s，沿与x轴正方向成α=60°角射入磁场，经电场偏转最终通过x轴上的Q点（图中未标出），不计粒子重力。求：
⑴带电粒子在磁场中运动的半径和时间；
⑵当电场左边界与y轴重合时Q点的横坐标；
⑶若只改变上述电场强度的大小，要求带电粒子仍能通过Q点，讨论此电场左边界的横坐标x′与电场强度的大小E′的函数关系。
如图所示，水平传送带以4 m/s的速度匀速运动，传送带两端A、B间的距离为20 m。现将一质量为2 kg的木块无初速地放在A端，木块与传送带间的动摩擦因数为0.2，g取10 m/s2，求木块从A端运动到B端所用的时间。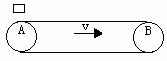
质量为3 kg的物体，在0 ~ 4 s内受水平力F的作用，在4 ~ 10 s内因受摩擦力作用而停止，其v-t图象如图所示。求：
（1）物体所受的摩擦力。
（2）在0 ~ 4 s内物体所受的拉力。
（3）在0 ~ 10 s内物体的位移。
水平桌面上质量为1 kg的物体受到2 N的水平拉力，产生1.5 m/s2的加速度。若水平拉力增至4 N，则物体将获得多大的加速度？
如图所示，传递带与水平面夹角θ=37°，并以v0=10m/s的速度运行着，在传送带的A端轻轻地放一小物体。若已知该物体与传送带
之间的滑动摩擦因数为μ=0.5，传送带A端到B端的距离S=16m，则小物体从A端运动到B端所需的时间可能是多少？（g=10m/s2）
三根不可伸长的相同的轻绳，一端系在半径为r0的环1上，彼此间距相等，绳穿过半径为r0的第2个圆环，另一端同样地系在半径为2r0的环3上，如图所示，环1固定在水平面上，整个系统处于平衡状态.试求第2个环中心与第3个环中心之间的距
离.(三个环都是用相同
的金属丝制作的，摩擦不计)