如图所示，有界匀强磁场的磁感应强度为B，区域足够大，方向垂直于纸面向里，直角坐标系xoy的y轴为磁场的左边界，A为固定在x轴上的一个放射源，内装镭核（
）沿着与+x成
角方向释放一个
粒子后衰变成氡核（
）。粒子在y轴上的N点沿
方向飞离磁场，N点到O点的距离为l，已知OA间距离为
，粒子质量为m，电荷量为q，氡核的质量为
。
（1）写出镭核的衰变方程；
（2）如果镭核衰变时释放的能量全部变为粒子和氡核的动能，求一个原来静止的镭核衰变时放出的能量。
在倾角为37°的斜面上，从A点以6m/s的初速度水平抛出一个小球，小球落在B点。如图所示，求小球刚碰到斜面时的速度方向（可用速度与水平方向夹角的正切表示）、AB两点间的距离和小球在空中飞行的时间。（g=10m/s2）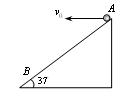
小球被轻质细绳系住斜吊着放在静止的光滑斜面上，小球质量m=0.5kg，斜面倾角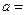
30°，悬线与竖直方向夹角为
30°，光滑斜面置于粗糙水平面上，整个装置处于静止状态。求悬线对小球拉力的大小。（g =10m/s2）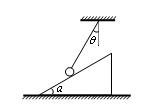
在如图所示的直角坐标系中，一、四象限存在垂直于纸面向里的匀强磁场，磁感应强度为B，二、三象限存在沿y轴负方向的匀强电场。现有一质量为m、电量为q的带点粒子从x轴负半轴上坐标为(-x , 0 )的位置出发开始运动，速度大小为v0，方向沿x轴正方向，粒子只受电场和磁场力的作用。若要粒子能够回到出发点，电场强度应为多大？粒子需多长时间回到出发点？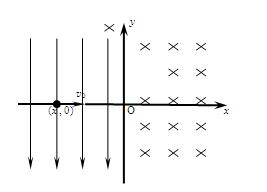
如图所示为水平面内的两条相互平行的光滑金属导轨，电阻可以忽略不计，轨道间距为l。导轨所处水平面内存在着竖直方向的匀强磁场，磁感应强度为B。两导体杆a和b垂直于导轨放置，它们的质量分别为m和2m，电阻分别为r和2r。现给导体杆a一沿导轨方向的初速度v0，若两杆始终都只能沿导轨方向运动，且除匀强磁场外其他磁场不计，试求：当杆a的速度减为v0/2时
(1)两导体杆的加速度分别为多大？
(2)两杆上分别产生了多少焦耳热？
(3)已经有多少电量流过了杆a？两导体杆间距相比最初增加了多少？
某一直流电动机提升重物的装置如图所示，重物的质量m=5kg，g=9.8m/s2，电源提供的电压U=110V，不计一切摩擦，当电动机以v=0.9m/s的恒定速度向上提升重物时，电路中的电流I=0.5A，求：
(1)由此可知电动机线圈的电阻R是多少？
(2)电动机的反电动势为多少？