某公司有
型产品40件，
型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：
| |
型利润 |
型利润 |
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
（1）设分配给甲店型产品
件，这家公司卖出这100件产品的总利润为
（元），求关于的函数关系式，并求出的取值范围；
（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；
（3）为了促销，公司决定仅对甲店型产品让利销售，每件让利
元，但让利后型产品的每件利润仍高于甲店型产品的每件利润．甲店的型产品以及乙店的
型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？
已知△ABC的一条边BC的长为5，另两边AB、AC的长是关于x的一元二次方程x2－(2k+3) x+k2+3k+2=0的两个实数根．
(1)求证：无论k为何值时，方程总有两个不相等的实数根．
(2)k为何值时，△ABC是以BC为斜边的直角三角形．
如图在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E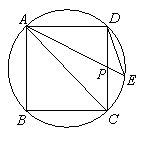
（1）写出同圆中一对不全等的相似三角形，并说明理由
（2）求弦DE的长。
解方程（4′×2=8′）
（1）5x（x+3）=2（x+3）（2）3x2－6x+2=0
计算（9ˊ）
（1）
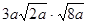（a≥0）（2）
（3）
为鼓励节约用电，某地用电收费标准规定：如果每月每户用电不超过150度，那么每度电0.5元；如果该月用电超过150度，那么超过部分每度电0.8元.
（1）如果小张家一个月用电128度，那么这个月应缴纳电费多少元？
（2）如果小张家一个月用电a度
，那么这个月应缴纳电费多少元？（用含a的代数式表示）
（3）如果这个月缴纳电费为147.8元，那么小张家这个月用电多少度？