已知二次函数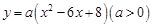
的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．
(1)如图①，连接AC，将△OAC沿直线AC翻折，若点O的对应点O'恰好落在该抛物线的对称轴上，求实数a的值；
(2)如图②，在正方形EFGH中，点E、F的坐标分别是（4，4）、（4，3），边HG位于边EF的右侧．若点P是边EF或边FG上的任意一点，求证四条线段PA、PB、PC、PD不能构成平行四边形；
(3)如图②，正方形EFGH向左平移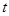
个单位长度时，正方形EFGH上是否存在一点P（包括正方形的边界），使得四条线段PA、PB、PC、PD能够构成平行四边形？如果存在，请求出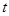的取值范围．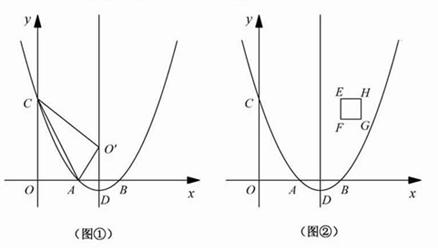
（本题10分）某农户承包果树若干亩，今年投资13800元，收获水果总产量为18000千克．此水果在市场上每千克售
元，在果园直接销售每千克售
元（＜）．该农户将水果拉到市场出售平均每天出售1000千克，需2人帮忙，每人每天付工资100元，农用车运费及其他各项税费平均每天200元．
（1）分别用含，
的代数式表示两种方式出售水果的收入．
（2）若=4．5元，=4元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．
（3）该农户加强果园管理，力争到明年纯收入达到72000元，而且该农户采用了（2）中较好的出售方式出售，那么纯收入增长率是多少（纯收入=总收入－总支出）？
（本题8分）某工艺厂计划一周生产工艺品2100个，平均每天生产300个，但实际每天生产量与计划相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减（单位：个） |
+5 |
-2 |
-5 |
+15 |
-10 |
+16 |
-9 |
（1）根据记录的数据，该厂星期一生产工艺品的数量为个；
（2）根据记录的数据，该厂本周产量最多的一天比最少的一天多生产个工艺品；
（3）该工艺厂在本周实际生产工艺品的数量为个；
（4）已知该厂实行每周计件工资制，每周结算一次，且每生产一个工艺品可得60元，若超额完成任务，则超过部分每个另奖50元，少生产一个扣80元．试求该工艺厂在这一周应付出的工资总额．
（本题4分）先化简再求值:
，其中
（本题6分）已知：
（本题6分）化简：
（1）
（2）