如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.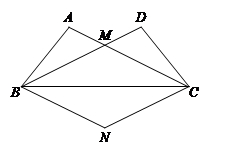
求证:△ABC≌△DCB
过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
.(8分)如图,四边形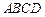 是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。
是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为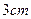 ,
,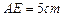 ,求∠ADE的正弦值.
,求∠ADE的正弦值.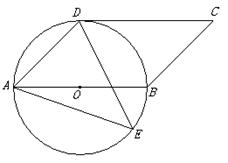
如图,有两个可以自由转动的均匀转盘 、
、 ,转盘
,转盘 上一条直径与一条半径垂直,转盘
上一条直径与一条半径垂直,转盘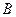 被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
①分别转动转盘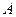 与
与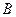
 ;
;
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止);
③如果和为0,则小明获胜;否则小刚获胜.
(1)用列表法(或树状图)求小明获胜的概率;
(2)你认为这个游戏对双方公平吗?如果你认为不公平,请适当改动规则使游戏对双方公平.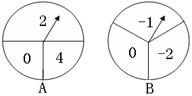
( 8分)某校组织学生到外地进行综合实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了 解,甲种汽车每辆最多能载40人和10件行李,乙种汽车
解,甲种汽车每辆最多能载40人和10件行李,乙种汽车 每辆最多能载30人和20件行李.
每辆最多能载30人和20件行李.
⑴如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
⑵如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案
如图,在3×3的正方形网格中,每个网格都有三个小正方形被涂黑.
(1)在图①中将一个空白部分的小正方形涂黑,使其余空白部分是轴对称图形但不是中心对称图形.
(2)在图②中将两个空白部分的小正方形涂黑,使其余空白部分是中心对称图形但不是轴对称图形.
.(6分)一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm(点A 、B、C在同一直线上),点A到地面的距离AD=8cm,旅行箱与水平面AE成50°角,求拉杆伸长到最大时,把手处C到地面的距离(精确到1cm).(参考数据:sin50°= 0.77,cos50°= 0.64,tan50°= 1.19.)
、B、C在同一直线上),点A到地面的距离AD=8cm,旅行箱与水平面AE成50°角,求拉杆伸长到最大时,把手处C到地面的距离(精确到1cm).(参考数据:sin50°= 0.77,cos50°= 0.64,tan50°= 1.19.)