如图15所示,平行金属导轨与水平面间夹角均为θ= 370 ,导轨间距为 lm ,电阻不计,导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg,电阻都是 1Ω ,与导轨垂直放置且接触良好,金属棒a’b’和导轨之间的动摩擦因数为0.5 ,金属棒ab和导轨无摩擦,导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场,导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场,磁感应强度 B 的大小相同.让a’ b’固定不动,将金属棒ab 由静止释放,当 ab 下滑速度达到稳定时,整个回路下滑速度达到稳定时,整个回路消耗的电功率为 18W 。求 :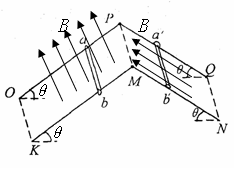
( 1 ) ab 达到的最大速度多大?
( 2) ab 下落了 30m 高度时,其下滑速度已经达到稳定,则此过程中回路电流的发热量 Q 多大?
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除,为确保a ' b’始终保持静止,则a ' b’固定解除时ab棒的速度有何要求? ( g ="10m" / s2 , sin370 ="0.6" ,cos370 ="0.8" )
用双缝干涉测光的波长。实验装置如图8(甲)所示,已知单缝与双缝间的距离L1=100mm,双缝与屏的距离L2=700mm,双缝间距d=0.25mm。用测量头来测量亮纹中心的距离。测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心如图8(乙)所示,记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数。
(1)分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如图8(丙)所示,则对准第1条时读数x1=_______mm、对准第4条时读数x2=_______mm
(2)写出计算波长λ的表达式,λ=_________(用符号表示),λ=_____nm
如图7所示,半球形玻璃砖的平面部分水平,底部中点有一小电珠。利用游标卡尺(或直尺)测量出有关数据后,可计算玻璃的折射率。试完成以下实验步骤:
(1)若S发光,则在玻璃砖平面上方看到平面中有一圆形亮斑。用游标卡尺测出_______________和______________(写出对应字母和其表示的意义)。
(2)写出玻璃折射率的表达式__________(用上述测量的物理量字母表示)。
某学习小组设计了如图3甲所示的测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机的转轴上,在电动机的带动下匀速转动。在圆形卡纸的旁边安装了一个改装了的电火花计时器,具体实验步骤如下:
①使电火花计时器与圆形卡纸保持良好接触;
②启动电动机,使圆形卡纸转动起来;
③接通计时器的开关,使它正常工作;④多打几个卡纸,选取点迹清晰卡纸(如图3乙所示),推导角度的表达式,得出角速度的测量值。
(1)要得到角速度的测量值,还缺少一个必要的测量工具,它是()
| A.秒表 | B.毫米刻度尺 | C.圆规 | D.量角器 |
(2)推导角速度的表达式,各量的物理意义是。
在用自由落体运动做“验证机械能守恒定律”实验中,用天平称得重物的质量为 ,所用电源的频率为50Hz,某同学通过正确的实验操作得到了一条理想的纸带。纸带上打出的点如图15所示(纸带上的O点是第一个打印点,A、B、C、D、E分别是每打两个点的时间作为计时单位取的记数点,图中数据单位为毫米),已知当地的重力加速度
,所用电源的频率为50Hz,某同学通过正确的实验操作得到了一条理想的纸带。纸带上打出的点如图15所示(纸带上的O点是第一个打印点,A、B、C、D、E分别是每打两个点的时间作为计时单位取的记数点,图中数据单位为毫米),已知当地的重力加速度 。选择B点为初始点,D点为终点,则从打下B点到打下D点的过程中,重物的重力势能的减少量为
。选择B点为初始点,D点为终点,则从打下B点到打下D点的过程中,重物的重力势能的减少量为 J;重物动能的增加量为
J;重物动能的增加量为 J;但实验中总存在△Ep△Ek(填:小于、等于、大于),其原因是。(取3位有效数字)
J;但实验中总存在△Ep△Ek(填:小于、等于、大于),其原因是。(取3位有效数字)
要测量电压表V1的内阻r。现有如下器材:
| A.待测电压表V1(量程3V,内阻约几千欧) |
| B.电压表 V2(量程15V,内阻约30kΩ ) |
| C.定值电阻R(3.0kΩ) |
| D.滑动变阻器R1(0~10Ω) |
E.直流电源E(电动势约9V,内阻约2Ω)
F.开关S及导线若干。
⑴因为所给V1、V2的内阻及定值电阻R都很大,即使它们并联所得电阻也很大,故最大值为10Ω的滑动变阻器在电路中必须使用 接法(填“分压”或“限流”)才能对电路起到控制作用;
⑵待测电压表V1两端的电压值可以由V1的示数直接读出,通过V1的电流因缺少电流表而不能直接测量,但可以借助题中给出的定值电阻R、电压表V2间接测出。为了测出通过V1的电流,甲、乙、丙三位同学分别设计了如图所示三种电路,其中合理的是 同学设计的电路。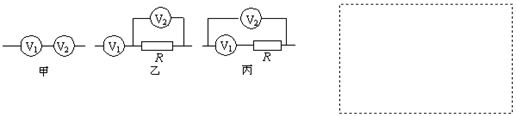
⑶在虚线框内画出测量电压表V1内阻r的完整的实验电路图;
⑷用已知量和直接测得量表示电压表V1内阻的表达式r=___________;式中各直接测得量的意义是: 。