如图所示,在倾角 =30o的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球A和B,两球之间用一根长L=0.2m的轻杆相连,小球B距水平面的高度h=0.1m。两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10m/s2。则下列说法中正确的是( )
=30o的光滑固定斜面上,放有两个质量分别为1kg和2kg的可视为质点的小球A和B,两球之间用一根长L=0.2m的轻杆相连,小球B距水平面的高度h=0.1m。两球从静止开始下滑到光滑地面上,不计球与地面碰撞时的机械能损失,g取10m/s2。则下列说法中正确的是( )
| A.下滑的整个过程中A球机械能守恒 |
| B.下滑的整个过程中两球组成的系统机械能守恒 |
| C.两球在光滑水平面上运动时的速度大小为2 m/s |
D.系统下滑的整个过程中B球机械能的增加量为 J J |
许多科学家在物理学发展过程中做出了重要贡献,下列叙述中符合物理学史实的是
| A.牛顿提出了万有引力定律,通过实验测出了万有引力常量 |
| B.奥斯特发现了电流的磁效应,法拉第通过实验总结出了电磁感应定律 |
| C.库仑在前人研究的基础上通过扭秤实验研究得出了库仑定律 |
| D.哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律 |
如图所示,理想变压器原线圈中正弦式交变电源的输出电压和电流分别为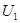 和
和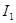 ,两个副线圈的输出电压和电流分别为
,两个副线圈的输出电压和电流分别为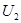 和
和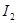 、
、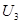 和
和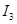 .接在原副线圈中的五个完全相同的灯泡均正常发光。则下列表述正确的是
.接在原副线圈中的五个完全相同的灯泡均正常发光。则下列表述正确的是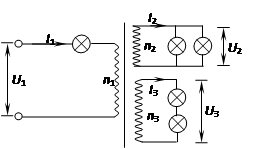
A 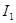 ∶
∶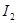 ∶
∶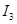 =1∶2∶1
=1∶2∶1
B 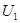 ∶
∶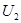 ∶
∶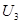 =1∶1∶2
=1∶1∶2
C 三个线圈匝数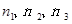 之比为5∶2∶1
之比为5∶2∶1
D 电源电压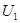 与原线圈两端电压
与原线圈两端电压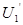 之比为5∶4
之比为5∶4
狄拉克曾经预言,自然界应该存在只有一个磁极的磁单极子,假设地面附近空中有一S 极磁单极子,在竖直平面内的磁感线如图所示,一带电微粒正在该磁单极子附近的水平面上做匀速圆周运动,图中①②③表示三个不同的水平面,则该微粒所在平面可能是图中的
A平面① B平面② C平面③ D平面①②都可能
电子体重秤的原理图如图中的虚线所示,它主要由三部分构成:踏板、压力传感器R(是一个阻值可随压力大小而变化的电阻器)、显示体重的仪表G(实质是理想电流表).设踏板的质量可忽略不计,已知理想电流表的量程为3A,电源电动势为12V,内阻为2Ω,电阻R随踏板变化的函数式为R =30–0.02F(F和R的单位分别是N和Ω).下列说法正确是
A 该秤能测量的最大体重是1400N
B 该秤能测量的最大体重是1300N
C 该秤零刻度线(即踏板空载时的刻度线)应标在电流表G刻度盘0.375A处
D 该秤零刻度线(即踏板空载时的刻度线)应标在电流表刻度盘0.400A处
如图,质量为M、长度为l的小车静止在光滑的水平面上.质量为m的小物块(可视为质点)放在小车的最左端.现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动.物块和小车之间的摩擦力为Ff.物块滑到小车的最右端时,小车运动的距离为s.在这个过程中,以下结论正确的是
A 物块到达小车最右端时具有的动能为F (l+s)
B 物块到达小车最右端时,小车具有的动能为Fs
C 物块克服摩擦力所做的功为Ff (l+s)
D 物块和小车增加的机械能为F (l+s)-Ff l