设椭圆 ,直线
,直线 过椭圆左焦点
过椭圆左焦点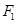 且不与
且不与 轴重合,
轴重合,  与椭圆交于
与椭圆交于 ,两点,当
,两点,当 与
与 轴垂直时,
轴垂直时, ,若点
,若点 且
且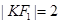
(1)求椭圆 的方程;
的方程;
(2)直线 绕着
绕着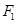 旋转,与圆
旋转,与圆 交于
交于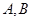 两点,若
两点,若 ,求
,求 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。
已知椭圆 的中心在原点,焦点在轴 上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为 ).
(Ⅰ)求椭圆
的方程;
(Ⅱ)设点
是椭圆
的左准线与
轴的交点,过点
的直线
与椭圆
相交于
,
两点,当线段
的中点落在正方形
内(包括边界)时,求直线
的斜率的取值范围。
已知函数 ,其中
,其中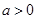
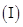 若
若 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值; 求
求 的单调区间;
的单调区间;
(Ⅲ)若 的最小值为1,求a的取值范围。
的最小值为1,求a的取值范围。
在数列 中,
中,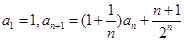
(I)设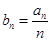 ,求数列
,求数列 的通项公式
的通项公式
(II)求数列 的前
的前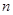 项和
项和
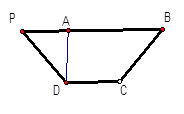
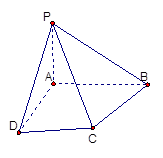
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=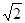 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分 .
.
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5. 同时投掷这两枚玩具一次,记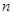 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(Ⅰ)求事件“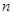 不大于6”的概率;
不大于6”的概率;
(Ⅱ)“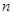 为奇数”的概率和“
为奇数”的概率和“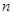 为偶数”的概率是不是相等?证明你的结论.
为偶数”的概率是不是相等?证明你的结论.