如图，一转盘被等分成三个扇形，上面分别标有-1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，某个扇形会恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）．
（1）若小静转动转盘一次，求得到负数的概率；
（2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”．用列表法（或画树状图）求两人“不谋而合”的概率．
如图，正方形ABCD中,P是AC上一点，E是BC延长线上一点,且PB=PE．若BP=
，求DE的长．
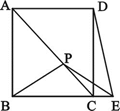
某学校后勤人员到一家文具店给九年级的同学购买考试用文具包．文具店规定一次购买400个以上，可享受8折优惠，若给九年级学生每人购买一个，不能享受8折优惠，需付款1936元；若多买88个，就可享受8折优惠，同样只需付款1936元．请问该学校九年级学生有多少人？
某校有学生2100人,在“文明我先行”的活动中,开设了“法律、礼仪、感恩、环保、互助”五门校本课程,规定每位学生必须且只能选择一门。为了解学生的报名意向学校随机调查了100名学生,并制成如右统计表:
（1）在这次调查活动中,学校采取的调查的方式是（填写“普查”或“抽样调查”）
（2）a=，b=，m=．
（3）如果要画“校本课程报名意向扇形统计图”，那么“礼仪”类校本课程所对应的扇形圆心角的度数是．
（4）请你统计，全校选择“感恩”类校本课程的学生约有人．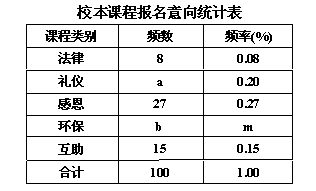
解不等式
＜1，并把它的解集在数轴上表示出来．
如图，在平面直角坐标系xOy中，点A(
，0)，点B(0，2)，点C是线段OA的中点．
（1）点P是直线AB上的一个动点，当PC+PO的值最小时，
①画出符合要求的点P（保留作图痕迹）；
②求出点P的坐标及PC+PO的最小值；
（2）当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时，求a的值并指出这个公共点所在象限．