在高能物理研究中，粒子回旋加速器起着重要作用，如图甲为它的示意图。它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条窄缝。两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中。在磁场力的作用下运动半周，再经狭缝电压加速。如此周而复始，最后到达D型盒的边缘，获得最大速度，由导出装置导出。已知正离子的电荷量为q，质量为m，加速时电极间电压大小为U，磁场的磁感应强度为B，D型盒的半径为R。每次加速的时间很短，可以忽略不计。正离子从离子源出发时的初速度为零，求
（1）为了使正离子每经过窄缝都被加速，求交变电压的频率
（2）求离子能获得的最大动能
（3）求离子第1次与第n次在下半盒中运动的轨道半径之比。
(18分)如图所示，有一个竖直固定在地面的透气圆筒，筒中有一轻弹簧，其下端固定，上端连接一质量为m的薄滑块，当滑块运动时，圆筒内壁对滑块有阻力的作用，阻力的大小恒为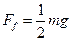
(g为重力加速度)．在初始位置滑块静止，圆筒内壁对滑块的阻力为零，弹簧的长度为l．现有一质量也为m的物体从距地面2l处自由落下，与滑块发生碰撞，碰撞时间极短．碰撞后物体与滑块粘在一起向下运动，运动到最低点后又被弹回向上运动，滑动到初始位置时速度恰好为零，不计空气阻力．求：
（1）物体与滑块碰撞过程中，合力对物体的冲量的大小；
（2）碰撞后，在滑块向下运动到最低点的过程中弹簧弹力所做的功．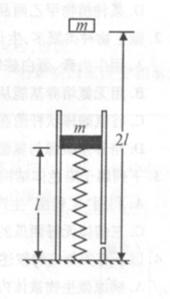
(16分)如图所示，传送带右端有一与传送带等高的光滑水平面，一行李包(可视为质点)以一定的初速度v0向左滑上传送带．传送带逆时针转动，速度为v=4m/s，且v<v0．已知行李包与传送带间的动摩擦因数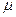
=0．20，当传送带长度为L="12" m时，行李包从滑上水平传送带的右端到左端的时间刚好为t="2" s皮带轮与皮带之间始终不打滑．不计空气阻力，g取10 m／s2．求行李包的初速度vo．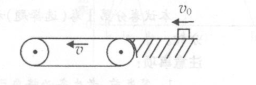
两质量分别为M1和M2的劈A和B，高度相同，放在光滑水平面上，A和B的倾斜面都是光滑曲面，曲面下端与水平面相切，如图所示，一质量为m的物块位于劈A的倾斜面上，距水平面的高度为h。物块从静止滑下，然后又滑上劈B。求物块在B上能够达到的最大高度。
一列横波在两个时刻的波形如图所示（
（1）由图所示读出波的振幅和波长；
（2）设周期大于
，如波是向右传播的，波速多大？如波是向左传播的，波速多大？
（3）设周期小于，且波速为6000米/秒，这列波传播方向如何？
两木块A，B质量分别为ｍ，M，用劲度系数为Ｋ的轻弹簧连在一起，放在水平地面上．如图所示，用外力将木块A压下一段距离静止，释放后A做简谐运动．在A的振动过程中，木块B刚好始终未离开地面，求：
（1）木块A的最大加速度；
（2）木块B对地面的最大压力；
（3）要使B离开地面，外力至少多大？