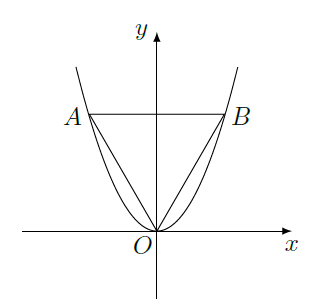
如图，等边三角形
的边长为
，且其三个顶点均在抛物线
上。
（1）求抛物线
的方程；
（2）设动直线
与抛物线
相切于点
，与直线
相交于点
，证明以
为直径的圆恒过
轴上某定点.
（本小题满分13分）已知数列
的前n项和为
，
（
），
．
（1）当t为何值时，数列
是等比数列？
（2）设数列
的前n项和为
， 
，点
在直线
上，在（1）的条件下，若不等式
对于
恒成立，求实数m的最大值．
（本小题满分12分）已知函数
在区间
上的值域为
．
（1）求函数
的单调递增区间；
（2）在△ABC中，角A，B，C所对的边长分别为a，b，c，当m＞0时，若
，
，△ABC的面积为
，求边长a的值．
（本小题满分12分）
已知函数
在点
处的切线方程是
，其中
是自然对数的底数．
（1）求实数a、b的值；
（2）求函数
在区间
上的值域．
（本小题满分12分）已知向量
，
，
，且
．
（1）求
；
（2）设向量
与
的夹角为
，求
的值．
（本小题满分12分）
在各项均为正数的等比数列
中，
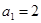，且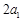
，
，
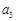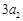成等差数列．
（1）求等比数列的通项公式；
（2）若数列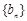
满足
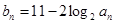，求数列
的前n项和
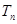的最大值.