如图，在正方形网格中，△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．
（1）以点O（0，0）为位似中心，按比例尺3:1在位似中心的同侧将△OAB放大为△OA’B’，放大后点A、B的对应点分别为A’、B’ ．画出△OA’B’，并写出点A’、B’的坐标：A’（ ），B’（ ）．
（2）在（1）中，若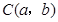
为线段
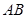上任一点，写出变化后点
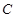的对应点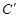
的坐标 （ ）．
如图，这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图，但负责画此图的同学忘记了最喜爱篮球运动的人生．
（1）请你求出图中的x值；
（2）如果该年级最喜爱跳绳运动的同学有144人，那么这个年级共有多少人？
如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC=4，CD=5．
（1）求DB的长；
（2）在△ABC中，求BC边上高的长．
如图，小黄和小陈观察蜗牛爬行，蜗牛在以A为起点沿直线匀速爬向B点的过程中，到达C点时用了6分钟，那么还需要多长时间才能到达B点？
计算：
．
在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．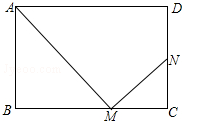
（1）求证：△CMN∽△BAM；
（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；
（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．