计算: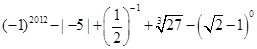 .
.
某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
某商品售价为每件9万元,为了参与市场竞争,商店按售价的九折再让利4000元销售,此时仍可获得10%的利润,此商品的进价是多少万元?
一项工程甲单独完成需要20小时,乙单独完成需要12小时,则甲先做8小时,然后甲乙合作,完成了这项工程的 ,则从开始到现在甲做了多少小时?
,则从开始到现在甲做了多少小时?
已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是多少?
先化简,再求值: ,其中
,其中 满足
满足 .
.