已知函数
(I) 讨论
的单调性;
(II)设
有两个极值点
若过两点
的直线I与
轴的交点在曲线
上,求
的值。
(本小题满分14分).如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC的中点,且DE∥BC.
(1)求证:DE∥平面ACD
(2)求证:BC⊥平面PAC;
(3)求AD与平面PAC所成的角的正弦值;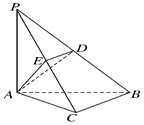
(本小题满分14分)
已知函数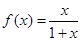
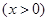 ,数列
,数列 满足:
满足: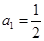 ,
,
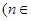 N*
N*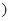 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令函数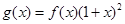 ,数列
,数列 满足:
满足: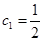 ,
, N*),
N*),
求证:对于一切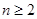 的正整数,都满足:
的正整数,都满足: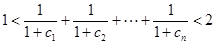 .
.
(本小题满分14分)
已知函数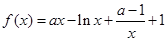 .
.
(1)当 时,求曲线
时,求曲线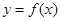 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,讨论
时,讨论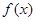 的单调性.
的单调性.
(本小题满分14分)
如图,在四棱锥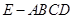 中,
中,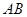 ⊥平面
⊥平面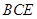 ,
,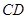 ⊥平面
⊥平面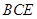 ,
,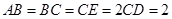 ,
,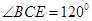 。
。
(1)求证:平面ADE⊥平面ABE;
(2)求二面角A—EB—D的余弦值.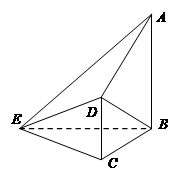
(本小题满分14分)
已知数列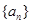 的前
的前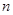 项和
项和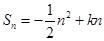 ,
,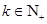 ,且
,且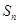 的最大值为8.
的最大值为8.
(1)确定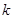 的值;
的值;
(2)求数列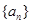 的通项公式;
的通项公式;
(3)求数列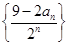 的前
的前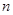 项和
项和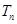 .
.