如图，在梯形ABCD中，AD∥BC，E是BC上的一点，且CE＝8，BC＝12，CD＝4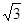
，∠C＝30°，∠B＝60°。点P是线段BC边上一动点（包括B、C两点），设PB的长是x。
（1）当x为何值时，以点P、A、D、E为顶点的四边形为直角梯形。
（2）当x为何值时，以点P、A、D、E为顶点的四边形为平行四边形。
（3）P在BC 上运动时，以点P、A、D、E为顶点的四边形能否为菱形。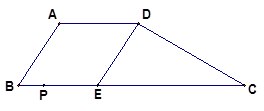
计算：
计算：
计算：
已知多项式
中，含字母的项的系数为
，多项式的次数为
．常数项为
，且、、分别是点A、B、C在数轴上对应的数．
（1）求、、的值，并在数轴上标出A、B、C．
（2）若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动，它们的速度分别是
、2、
（单位长度／秒），当乙追上丙时，乙是否追上了甲?为什么?
（3）在数轴上是否存在一点P，使P到A、B、C的距离和等于10?若存在，请直接指出点P对应的数；若不存在，请说明理由．
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90％付款．
现某客户要到该服装厂购买西装20套，领带
条（>20）．
（1）若该客户按方案①购买，需付款________元（用含的代数式表示）；若该客户按方案②购买，需付款________元（用含的代数式表示）．
（2）若=30，通过计算说明此时按哪种方案购买较为合算?