在平面直角坐标系xoy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,
给出如下定义:
若∣x1-x2∣≥∣y1-y2∣,则点P1与点P2的“非常距离”为∣x1-x2∣;
若∣x1-x2∣<∣y1-y2∣,则点P1与点P2的“非常距离”为∣y1-y2∣.
例如:点P1(1,2),点P2(3,5),因为∣1-3∣<∣2-5∣,所以点P1与点P2的“非常距离”为
∣2-5∣=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x
轴的直线P2Q的交点)。
(1)已知点 ,B为y轴上的一个动点,
,B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线 上的一个动点,
上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最
小值及相应的点E和点C的坐标。

如图,C为线段BD上一动点,分别过点B,D作AB BD,ED
BD,ED BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
BD,连接AC,ED。已知AB=5,DE=1,BD=8,设CD=x。
(1)用含的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构造图形(给出必要的说明)求出代数式 的最小值。
的最小值。
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加。据统计,某小区2008年底拥有家庭轿车64辆,2010年底家庭轿车的拥有量达到100辆。
(1)若该小区2008年底2010年底家庭轿车拥有量的年平均增长率都相同,按2010年的增长率求该小区到2011年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位,据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案。
如图,在网格中有一个四边形图案。动手画一画: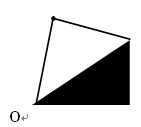
(1)请你画出此图案绕点O顺时针方向旋转900,1800,2700的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
动手算一算:(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1,A2,A3,,求四边形AA1A2A3的面积。
动脑想一想:(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论。
某西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克。为了促销,该经营户决定降价销售。经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克。另外每天的房租等固定成本共24元。该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
如图,在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).