已知抛物线
的顶点为P，与
轴交于点A，与直线OP交于点B.
（Ⅰ）如图1，若点P的横坐标为1，点B的坐标为（3，6），试确定抛物线的解析式；
（Ⅱ）在（Ⅰ）的条件下，若点M是直线AB下方抛物线上的一点，且
，求点M的坐标；
（Ⅲ）如图2，若点P在第一象限，且PA=PO，过点P作PD⊥
轴于点D.将抛物线平移，平移后的抛物线经过点A、D，该抛物线与轴的另一个交点为C，请探究四边形OABC的形状，并说明理由.
已知：□ABCD的两边AB，AD的长是关于x的方程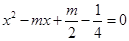
的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么□ABCD的周长是多少？
如图，已知二次函数y=x2+bx+c过点A（1，0），C（0，﹣3）．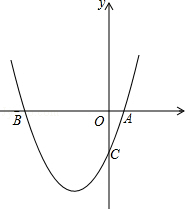
（1）求此二次函数的解析式；
（2）在抛物线上存在一点P使△ABP的面积为10，请求出出点P的坐标．
二次函数的图象经过点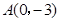
，
，
．
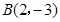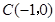（1）求此二次函数的关系式；
（2）求此二次函数图象的顶点坐标；
（3）填空：把二次函数的图象沿坐标轴方向最少平移个单位，使得该图象的顶点在原点．
关于x的一元二次方程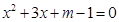
的两个实数根分别为
．
（1）求m的取值范围；
（2）若
，求m的值.
已知x1＝－1是方程x2＋mx－5＝0的一个根，求m的值及另一个根x2．