在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数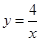 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x、y满足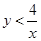 的概率.
的概率.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F。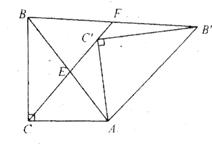
(1)若AC=3,AB=4,求
(2)证明:△ACE∽△FBE;
(3)设∠ABC= ,∠CAC′=
,∠CAC′= ,试探索
,试探索 、
、 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
| 型号 |
占地面积(m2/个) |
使用农户数(户/个) |
造价(万元/个) |
| A |
15 |
18 |
2 |
| B |
20 |
30 |
3 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户。
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱。
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米。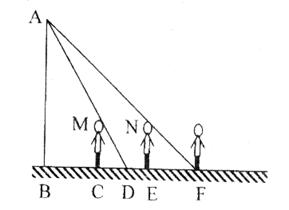
(1)求路灯A的高度;
(2)当王华再向前走2米,到达F处时,他的影长是多少?
初中生的视力状况受到社会的广泛关注,某市有关部门对全市3万名初中生的视力状况进行了一次抽样调查,下图是利用所得数据绘制的频数分布直方图,根据图中所提供的信息回答下列问题:
(1)本次调查共抽测了多少名学生?
(2)在这个问题中的样本指什么?
(3)如果视力在4.9-5.1(含4.9和5.1)均属正常,那么全市有多少名初中生视力正常?
如图,在12×12的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2)。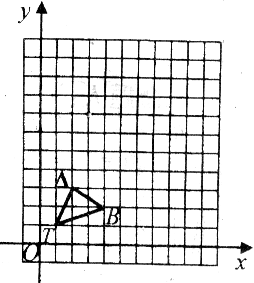
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1的位似中心的同侧将TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标。