从地球表面向火星发射火星探测器。设地球和火星都在同一平面上绕太阳做匀速圆周运动。火星轨道半径
为地球轨道半径
的1.5倍。简单而又比较节省能量的发射过程可分为两步进行：第一步，在地球表面用火箭对探测器进行加速，使之获得足够的动能，成为一个绕地球运行的人造卫星；第二步，在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速，使其速度数值增加到适当值，使探测器沿半个椭圆轨道（该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切）射到火星上。如图(a)所示。已知地球半径
，重力加速度g=10m/s2。
（1）为使探测器成为绕地球运行的人造卫星，探测器在地面附近至少要获得多大的速度(不考虑地球自转)。
（2）求火星探测器的飞行时间为多少天（已知
，1年为365天）。
（3）当探测器绕地球运行稳定后，在某年 3月 1 日零时测得探测器与火星之间的角度为 60°，如图(b)所示。求应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面(时间计算仅需精确到天，已知
，1年为365天)。
在粗糙水平轨道上，有一物块以初速度v0＝6m/s，向右做匀减速直线运动，其加速度a大小为4m/s2，求：物块运动了多长时间速度为零;
物块运动的前0.5s内位移的大小。
如图所示，圆管构成的半圆形竖直轨道固定在水平地面上，轨道半径为R，MN为直径且与水平面垂直，直径略小于圆管内径的小球A以某一初速度冲进轨道，到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞，碰后两球粘在一起飞出轨道，落地点距N为2R。重力加速度为g，忽略圆管内径，空气阻力及各处摩擦均不计，求：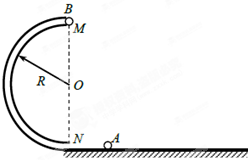
粘合后的两球从飞出轨道到落地的时间t；
小球A冲进轨道时速度v的大小。
小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动．当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地，如图所示．已知握绳的手离地面高度为d，手与球之间的绳长为d，重力加速度为g.忽略手的运动半径和空气阻力．
求绳断时球的速度大小v1和球落地时的速度大小v2.
问绳能承受的最大拉力多大？
改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？
如图，质量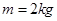
的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经
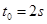拉至B处。(已知
，
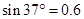。取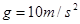
)求物体与地面间的动摩擦因数μ；
用大小为30N，与水平方向成37°的力斜向上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。
在研究摩擦力特点的实验中，将木块放在足够长的静止水平木板上．如图11甲所示，用力沿水平方向拉木块，使拉力F从0开始逐渐增大．经实验绘制出摩擦力Ff随拉力F的变化图象如图丙所示．已知木块质量为0.78 kg.
求木块与长木板间的动摩擦因数．
若木块在与水平方向成θ＝37°角斜向右上方的恒定拉力F′作用下，以a＝2.0 m/s2的加速度从静止开始做匀加速直线运动，如图乙所示．则F′为多大？
(取sin 37°＝0.6，cos 37°＝0.8)