如图所示,水平的平行虚线间距为d,其间有磁感应强度为B的匀强磁场。一个长方形线圈的边长分别为L1、L2,且L2<d,线圈质量m,电阻为R。现将线圈由静止释放,测得当线圈的下边缘到磁场上边缘的距离为h时,其下边缘刚进入磁场和下边缘刚穿出磁场时的速度恰好相等。求: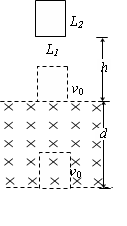
(1)线圈刚进入磁场时的感应电流的大小;
(2)线圈从下边缘刚进磁场到下边缘刚出磁场(图中两虚线框所示位置), 求该过程最小速度v;
(3)线圈其下边缘刚进入磁场一直到上边缘刚穿出磁场的全过程中产生的总焦耳热Q总。
如图所示,已知甲乙两质点沿直线运动,求: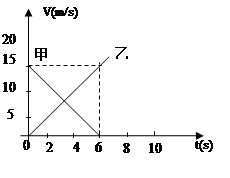
(1)两质点运动的初速度
(2)前6s内它们的速度变化量
(3)前6s内它们的加速度
一束电子流在经U=5000 V的加速电压加速后,在距两极板等距处以速度v0垂直进入平行板间的匀强电场,如图所示,若两板间距d="1.0" cm,板长l="5.0" cm,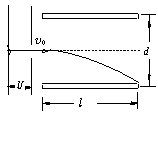
(1)当两极板所加电压一定时,电子能从平行板间飞出试证明电子的侧移量y与电子的电量m, 质量 q无关。
(2)要使电子能从平行板间飞出,两个极板上最多能加多大电压?
(3)要使电子能打在下板的中点A处,两个极板所加的电压?
如图所示,一长为L的细线上端固定,下端拴一质量为m的带电小球,将它置于一水平向右的匀强电场E中,当细线偏角为θ=450时,小球处于平衡状态,
试问:(1)小球的带电荷量q多大?
(2)若细线的偏角θ从450增加到900,然后由静止释放小球,细线到达竖直位置时小球速度?该位置绳子对球的拉力为多少?
.如图所示,一带电粒子从A点以v0的速度沿垂直电场线方向的直线AO方向射入电场,由B点飞出匀强电场时速度方向与AO方向成45°。已知粒子质量为m,电荷量为q。
(1)求AB两点间电势差。
(2)若将该匀强电场的场强增加一倍其余条件不变,求该粒子飞出匀强电场时速度方向与水平方向夹角的正切值
如图所示,匀强电场中,有a、b、c三点,ab=5cm,bc=12cm,其中ab沿电场方向,bc和电场方向成60º角,一个电荷量为q=4×10-8C的正电荷从a点移到b点,电场力做正功W1=1.2×10-7J,
求:(1)匀强电场的场强E;
(2)电荷从b移到c,电场力做的功W2;
(3)a、c两点间的电势差Uac。