如图所示，半径为R的半球形容器固定在水平面上，一质量为m的小球（可视为质点）由静止开始自容器边缘上的A点滑下，经过最低点B时，它对容器的正压力为
。已知重力加速度为g，则小球自A滑到B的过程中摩擦力对其所做的功为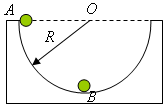
A． |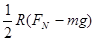
B． |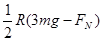
C． |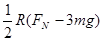
D． |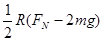
一列简谐横波在t=0时刻的波形图如图甲实线所示，若波传播的速度为10m/s，从此刻起，经0.1s波形图如图甲虚线所示，则（）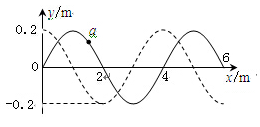
| A．这列波沿x轴正方向传播 |
| B．t=0时刻质点a沿y轴正方向运动 |
| C．x=2m处的质点的位移表达式为y = 0.2sin5πt（m） |
| D．从t=0时刻开始质点a经0.2s通过的路程为0.4m |
狄拉克曾经预言，自然界应该存在只有一个磁极的磁单极子。假设地面附近空中有一N极磁单极子，在竖直平面内的磁感线如图所示。一质量为m、电荷量为q的带电粒子正在该磁单极子上方附近沿顺时针方向（从轨迹上方朝下看）做速度大小为v、半径为R的匀速圆周运动，其轨迹如虚线所示，轨迹平面为水平面。若不考虑地磁场的影响，重力加速度大小为g，则下列说法正确的是
| A．该粒子带正电 |
| B．该粒子受到的洛伦兹力全部提供做匀速圆周运动的向心力 |
C．该粒子所在处磁感应强度大小为 |
D．该粒子所在处磁感应强度大小为 |
中国志愿者王跃参与人类历史上第一次全过程模拟从地球往返火星的试验“火星－500”．假设将来人类一艘飞船从火星返回地球时，经历如图所示的变轨过程，则下列说法正确的是
| A．飞船在轨道Ⅱ上运动时，在P点的速度大于在Q点的速度 |
| B．飞船在轨道Ⅰ上运动时，在P点的速度大于在轨道Ⅱ上运动时在P点的速度 |
| C．飞船在轨道Ⅰ上运动到P点时的加速度等于飞船在轨道Ⅱ上运动到P点时的加速度 |
| D．若轨道Ⅰ贴近火星表面，测出飞船绕火星在轨道Ⅰ上运动的周期，就可以推知火星的密度 |
如图所示的三个图线分别是用不同的传感器测出的不同物体的振动图线。图中心脏跳动的图线是某人的心电图，方格纸每个小方格的宽度是0.5 cm，心电图记录仪拖动方格纸的速度是1.8 cm/s。下列说法正确的是
| A．从三个图线可知，这三个物体振动的共同特点是具有周期性 |
| B．三个物体中，最简单的振动是声音的振动 |
| C．根据心电图可知，此人的心率是60次/分 |
| D．弹簧振子做简谐运动，振子相继两次通过同一位置时，摆球的动能必相同 |
如图所示，甲中有两条不平行轨道而乙中的两条轨道是平行的，其余物理条件都相同．金属棒MN都正在轨道上向右匀速平动，在棒运动的过程中，将观察到
| A．L1、L2小电珠都发光，只是亮度不同 |
| B．Ll、L2都不发光 |
| C．L2发光，Ll不发光 |
| D．Ll发光，L2不发光 |