如图所示,AOB是1/4圆柱玻璃砖的截面,玻璃砖的折射率为 。一束平行光以45°入射角射向玻璃砖的OA平面,这些光线中只有一部分能从圆柱的AB面上射出。假设凡射到OB面的光线全部被吸收,也不考虑OA面的反射作用,试求圆柱AB面上能射出光线的部分占AB表面的几分之几?
。一束平行光以45°入射角射向玻璃砖的OA平面,这些光线中只有一部分能从圆柱的AB面上射出。假设凡射到OB面的光线全部被吸收,也不考虑OA面的反射作用,试求圆柱AB面上能射出光线的部分占AB表面的几分之几?
直流电源的路端电压U="182" V。金属板AB、CD、EF、GH相互平行、彼此靠近。它们分别和变阻器上的触点a、b、c、d连接。变阻器上ab、bc、cd段电阻之比为1∶2∶3。孔O1正对B和E,孔O2正对D和G。边缘F、H正对。一个电子以初速度v0=4×106 m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1="2" cm,L2="4" cm,L3="6" cm。电子质量me="9." 1×10-31 kg,电量q=1.6×10-19 C。正对两平行板间可视为匀强电场,(不计电子的重力)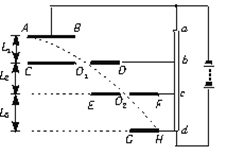
求:(1)各相对两板间的电场强度。
(2)电子离开H点时的动能。
(3)四块金属板的总长度(AB+CD+EF+GH)。
如图,一个质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点.已知圆弧的半径为R且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力.求:
(1)小球从A点做平抛运动的初速度v0的大小;
(2)在D点处管壁对小球的作用力N;
(3)小球在圆管中运动时克服阻力做的功Wf.
如图所示,足够长的斜面倾角=370,一物体以v0=24m/s的初速度从斜面上A点处沿斜面向上运动;加速度大小为a=8m/s2,g取10m/s2.求:
(1)物体沿斜面上滑的最大距离x;
(2)物体与斜面间的动摩擦因数μ;
(3)物体从A点出发需经多少时间才能回到A处.
(6分)气缸长为L=1m,固定在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞封闭了一定质量的理想气体,当温度为t=27℃,大气压为p0=1×105 Pa时,气柱长度为l=0.9m,气缸和活塞的厚度均可忽略不计.求:
①如果温度保持不变,将活塞缓慢拉至气缸右端口,此时水平拉力F的大小?
②如果气缸内气体温度缓慢升高,使活塞移至气缸右端口时,气体温度为多少摄氏度?
(19分)如图所示,边长为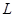 的正方形PQMN区域内(含边界)有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为
的正方形PQMN区域内(含边界)有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为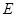 ,质量为
,质量为 、电荷量为
、电荷量为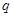 的带正电粒子从O点由静止开始释放,O、P、Q三点在同一水平直线上,OP=L,带电粒子恰好从M点离开磁场,不计带电粒子重力,求:
的带正电粒子从O点由静止开始释放,O、P、Q三点在同一水平直线上,OP=L,带电粒子恰好从M点离开磁场,不计带电粒子重力,求:
(1)磁感应强度大小 ;
;
(2)粒子从O点运动到M点经历的时间;
(3)若磁场磁感应强度可调节(不考虑磁场变化产生的电磁感应),带电粒子从边界NM上的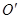 点离开磁场,
点离开磁场,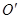 与N点距离为
与N点距离为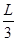 ,求磁场磁感应强度的可能数值.
,求磁场磁感应强度的可能数值.