牛顿以天体之间普遍存在着引力为依据,运用严密的逻辑推理,建立了万有引力定律。在创建万有引力定律的过程中,牛顿( )
| A.接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想 |
| B.根据地球上一切物体都以相同加速度下落的事实,得出物体受地球的引力与其质量成正比,即Fµm的结论 |
| C.根据Fµm和牛顿第三定律,分析了地月间的引力关系,进而得出Fµm1m2 |
| D.根据大量实验数据得出了比例系数G的大小 |
一电流表的满偏电流Ig=1mA,内阻为200Ω。要把它改装成一个量程为0.5A的电流表,则应在电流表上()
| A.并联一个200Ω的电阻 | B.并联一个0.4Ω的电阻 |
| C.串联一个0.4Ω的电阻 | D.串联一个200Ω的电阻 |
如图所示,电路中电源电动势为E,内电阻为r,定值电阻的阻值为R0,变阻器的全阻值为R,关于各部分的功率,有关说法正确的是:()
| A.当R=R0+r,R上消耗的功率达到最大值 |
| B.当R=R0+r,R0上消耗的功率达到最大值 |
| C.当R+R0=r,电源的输出功率达到最大值 |
| D.当R0=R+r,R0上消耗的功率达到最大值 |
有一横截面积为S的铜导线,流经其中的电流为I,设每单位体积的导线有n个自由电子,电子电量为e,此时电子的定向转动速度为υ,在△t时间内,通过导体横截面的自由电子数目可表示为:()
| A.nυS△t | B.nυ△t | C.I△t/e | D.I△t/(Se) |
如图所示为用直流电动机提升重物的装置,重物的重量为500N,电源电动势为110V,不计电源内阻及各处摩擦,当电动机以0.90m/s的恒定速度向上提升重物时,电路中的电流为5.0A,可以判断:()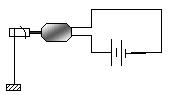
| A.电动机消耗的总功率为550W |
| B.提升重物消耗的功率为450W |
| C.电动机线圈的电阻为22Ω |
| D.电动机线圈的电阻为4Ω |
如图所示的电路中,电键S1、S2、S3、S4均闭合,C是极板水平放置的平行板电容器,极板间悬浮着一油滴P,欲使P向下运动,应断开电键( ) 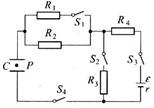
| A.S1 | B.S2 | C.S3 | D.S4 |