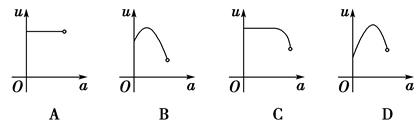
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是
a m(0<a<12)、4 m,不考虑树的粗细.现在想用16 m长的篱笆,借助墙角围成一个矩形的
花圃ABCD,设此矩形花圃的面积为S m2,S的最大值为f(a),若将这棵树围在花圃内,则函数
u=f(a)的图象大致是( )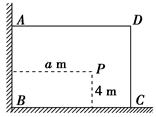
设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别为x=0,y=x,
则直线BC的方程是( )
| A.y=2x+5 | B.y=2x+3 |
| C.y=3x+5 | D.y=- x+ x+ |
若函数y=loga(x2-ax+1)有最小值,则a的取值范围是( )
| A.0<a<1 | B.0<a<2,a≠1 |
| C.1<a<2 | D.a≥2 |
.点P在曲线y=2x3-x+5上移动,设点P处切线倾斜角为α,则角α的取值范围是( )
A.[0,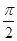 ] ] |
B.[0,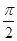 )∪[ )∪[ ,π) ,π) |
C.[ ,π) ,π) |
D.(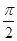 , , ] ] |
已知点 满足x+y≤6,y>0,x-2y≥0,则
满足x+y≤6,y>0,x-2y≥0,则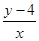 的最大值为( )
的最大值为( )
A.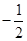 |
B. |
C.0 | D.不存在 |