一宇航员到达半径为R,密度均匀的某星球表面,做如下实验,用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图甲所示,在最低点给小球某一初速度,使其绕O点在竖直平面内做圆周运动,测得绳的拉力大小随时间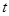 的变化规律如图乙所示,F1=7F2,设R、m、引力常量G、F1、F2均为己知量,忽略各种阻力,以下说法正确的是
的变化规律如图乙所示,F1=7F2,设R、m、引力常量G、F1、F2均为己知量,忽略各种阻力,以下说法正确的是
| A.小球在最高点的最小速度为零 |
B.卫星绕该星的第一宇宙速度为 |
C.该星球表面的重力加速度为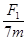 |
D.星球的质量为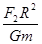 |
质量为M的斜面体放在水平地面上,质量为m1的物体放在斜面上,斜面的倾角为 ,质量为m2的物体用OA和OB两根绳子悬挂在空中,其中OA拴在m1上,且OA与斜面平行,OB恰好水平,则下列说法正确的是 ()
,质量为m2的物体用OA和OB两根绳子悬挂在空中,其中OA拴在m1上,且OA与斜面平行,OB恰好水平,则下列说法正确的是 ()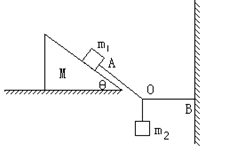
A.OA绳子的拉力大小等于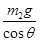 |
B.水平地面对M的支持力等于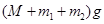 |
| C.OB绳的拉力大小等于地面对M的摩擦力 |
D.物体m1受到的摩擦力等于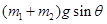 |
根据你对物理学的学习,一些科学思想和基本定义,下列说法正确的是()
| A.在国际单位制中规定长度、时间、力的单位为力学基本单位,它们的分别为m,s,N |
| B.已知分力求得合力采用等效的思想 |
C.电场强度的定义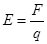 采用比值定义的方法 采用比值定义的方法 |
| D.牛顿首次提出“提出假说,数学推理,实验验证,合理外推”的科学推理方法 |
如图所示,两根光滑金属杆相距为L,用一段金属杆cd固连形成一个电阻可以忽略的U形框架,框架平面与水平面夹角为θ,处于一个范围足够大且与框架平面垂直的匀强磁场中,一根质量为m、电阻为R的金属棒ab垂直于平行金属杆搁置,用力F拉动棒ab沿斜面从静止开始以恒定加速度上滑,经过一段时间,撤去拉力F,金属杆ab开始减速上滑至最高点,则金属棒在()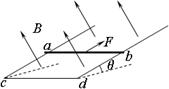
| A.匀加速上升时,拉力F是恒力 |
| B.减速上升时,金属棒的加速度逐渐增大 |
| C.减速上升过程中,安培力对金属棒所做的功等于棒机械能的增量 |
| D.匀加速上升过程中,拉力、重力和安培力做功之和等于棒动能的增量 |
如图甲所示,细绳跨过光滑的轻质定滑轮连接A、B两球,滑轮悬挂在一个传感器正下方,B球换用质量m不同的球,而A球始终不变,通过计算机描绘得到传感器拉力F随B球质量m变化的关系如图乙所示,F=F0直线是曲线的渐近线,已知轻质定滑轮质量可看成零,重力加速度为g,则()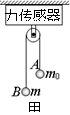
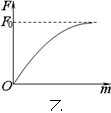
A.根据图线可以确定A球质量m0=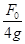
B.根据图线可以计算B球为某一质量m时其运动的加速度a
C.A、B球运动的加速度a一定随B质量m的增大而增大
D.传感器读数F一定小于A、B球总重力
如图所示,两个横截面分别为圆和正方形但磁感应强度均相同的匀强磁场,圆的直径d等于正方形的边长,两个电子分别以相同的速度飞入两个磁场区域,速度方向均与磁场方向垂直,进入圆形磁场区域的速度方向对准了圆心,进入正方形磁场区域的速度方向是沿一边的中垂线,则下面判断正确的是()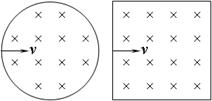
| A.两电子在两磁场中运动时半径相同 | B.两电子在两磁场中运动的时间一定不相同 |
| C.进入圆形磁场区域的电子一定先飞离磁场 | D.两电子在两磁场中偏转角度可能相同 |