如图,在平面直角坐标系中,直线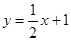 与抛物线
与抛物线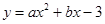 交于A,B两点,点A在
交于A,B两点,点A在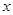 轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作
轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作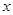 轴的垂线交直线AB与点C,作PD⊥AB于点D
轴的垂线交直线AB与点C,作PD⊥AB于点D
(1)求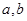 及
及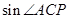 的值
的值
(2)设点P的横坐标为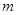
①用含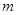 的代数式表示线段PD的长,并求出线段PD长的最大值;
的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把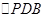 分成两个三角形,是否存在适合的
分成两个三角形,是否存在适合的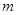 值,使这两个三角形的面积之比为9:10?若存在,直接写出
值,使这两个三角形的面积之比为9:10?若存在,直接写出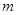 值;若不存在,说明理由.
值;若不存在,说明理由.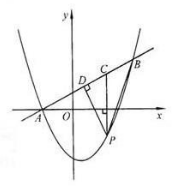
某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
马航MH370失联后,我国政府积极参与搜救.某日,我国两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75).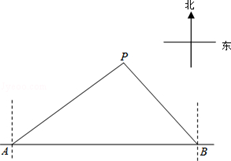
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).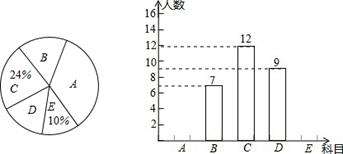
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
解不等式组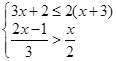 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
如图,已知抛物线y=—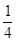 x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).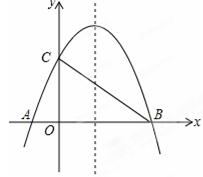
(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由