“体验·创新·成长”这是2012某市第八届少年科技大赛的宗旨.比赛分为四类:优秀科技实践活动、科技创新活动项目、优秀少儿科学幻想绘画、科技创新成果.评委对所有的参赛作品进行了分类统计,各类参赛作品按一定的百分比设奖,并对获奖作品也进行分类,制作了如下的条形统计图及扇形统计图:
作根据上述信息,完成下列问题:
(1) 参赛获奖品总数是 件;
(2) 算出获奖优秀科技实践活动所在扇形的圆心角的度数,并将条形图补充完整;
(3)全市中小学生参加少年科技大赛热情高涨,在2012参赛作品328件的基础上逐年增长,预计2014年参赛作品将有738件,求平均每年的增长率是多少?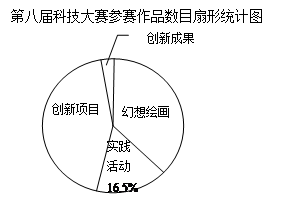

(·嘉兴市 第22题 12分)小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?
(·杭州市 第18题 8分)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M、N分别在AB、AC边上,AM=2MB,AN=2NC,求证:DM=DN
(·台州市 第21题 10分)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图: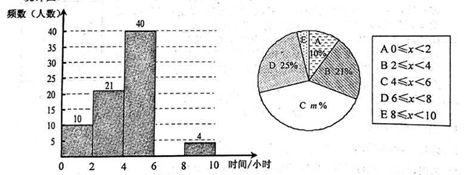
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
(·绍兴市 第19题 8分)为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图。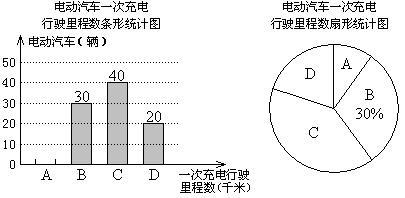
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
(·丽水市 第20题 8分)某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示: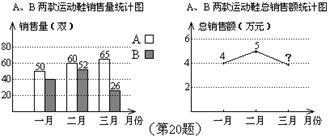
(1)一月份B款运动鞋的销售量是A款的 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。