在平面坐标系xoy中,直线 与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
(1)如图1,当点C与B重合时,连接OE求扇形EOA的面积;
(2)当 时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
(3)如图2,在转动中,过C作⊙E的切线,交y轴于D,当A,C,D,B四点围成的四边形是梯形时,求点D的坐标.
先化简,再求值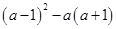 ,其中
,其中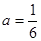 .
.
如图,在 中,
中,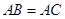 ,
,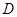 是
是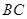 的中点,连接
的中点,连接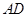 .
.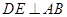 ,
,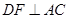 ,
, 是垂足.图中共有多少对全等三角形?请直接用“
是垂足.图中共有多少对全等三角形?请直接用“ ”符号把它们分别表示出来(不要求证明).
”符号把它们分别表示出来(不要求证明).
化简: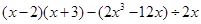
如图,一抛物线经过点A(−2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.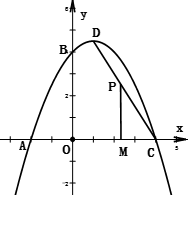
(1)求该抛物线的函数关系式及顶点D坐标.
(2)如图,若P为线段CD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAB的面积的最大值和此时点P的坐标.
(3)过抛物线顶点D,作DE⊥x轴于E点,F(m,0)是x轴上一动点,若以BF为直径的圆与线段DE有公共点,求m的取值范围.
如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.
(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.