从三个多项式：
，
，
中选择适当的两个进行加法运算，并把结果因式分解．
为体现社会对老师的尊重，教师节这一天上午，出租车司机小王在东西向的公路上免费接送老师，如果规定向东为正，向西为负，出租车的行程如下（单位：千米）
：+5，-4，+3，-10，+3，-9。
（1）最后一名老师送到目的时，小王距出租车出发点的距离是多少？
（2）若汽车耗油量为0.4升/千米，这天下午小王的汽车共耗油多少升？
先化简，再求值：
求代数式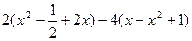
的值．其中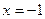
化简（每小
题5分，共10分）
(1) 
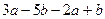（2）
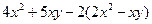
画出数轴，把下列各组数分别在数轴上表示出来，并用“＜”连接起来：
，2， 0，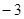
，
，
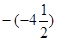
如图12，在△ABC中，AC=BC，∠B=30°，D是AC的中点，E是线段BC延长线上
一动点，过点A作AF∥BE，与线段ED的延长线交于点
F，连结AE、
CF.
（1）求证：AF=CE；
（2）若CE=
BC，试判断四边形AFCE是什么样的四边形，并证明你的结论；
（3）若CE= BC，求证：EF⊥AC.