探究与发现：
探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．
探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
已知：如图，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．
探究三：若将△ADC改为任意四边形ABCD呢？
已知：如图，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．
探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：_______________________________．
如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行（）
| A．8米 | B．10米 | C．12米 | D．14米 |
（本题10分）△ABC中，∠ACB＝90°，AC＝BC＝6，M点在边AC上，且CM＝2，过M点作AC的垂线交AB边于E点.动点P从点A出发沿AC边向M点运动，速度为每秒1个单位，当动点P到达M点时，运动停止.连接EP，EC.在此过程中，设P运动的时间为t秒，回答下列问题：
（1）AP=，PC=（用含t的代数式表示）
（2）当t为何值时，△EPC的面积为10？
（3））将△EPC沿CP翻折后，点E的对应点为F点，当t为何值时，PF∥EC？
（本题10分）在Rt△ABC中，∠CAB＝90°，AB＝AC．
（1）如图①，过点A在△ABC外作直线MN，BM⊥MN于M，CN⊥MN于N．
①判断线段MN、BM、CN之间有何数量关系，并证明；
②若AM＝
，BM＝
，AB＝
，试利用图①验证勾股定理
；
（2）如图②，过点A在△ABC内作直线MN，BM⊥MN于M，CN⊥MN于N，判断线段MN、BM、CN之间有何数量关系？（直接写出答案）
（本题6分）探索与应用．先填写下表，通过观察后再回答问题：
（1）表格中x＝；y＝；
（2）从表格中探究a与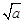
数位的规律，并利用这个规律解决下面两个问题：
①已知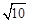
≈3.16，则
≈；
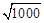②已知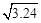
＝1.8，若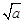＝180，则a＝.
（本题8分）如图，某住宅小区在施工过程中留下了一块空地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？