（1）探究新知：如图1，已知△ABC与△ABD的面积相等， 试判断AB与CD的位置关系，并说明理由．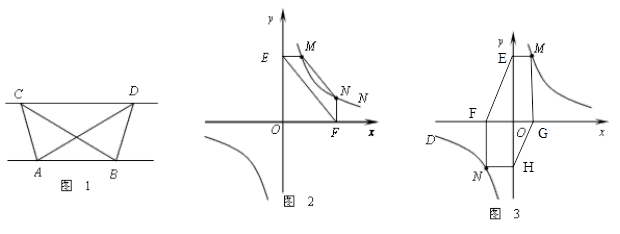 
（2）结论应用：如图2，点M，N在反比例函数
（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F． 试证明：MN∥EF．
（3）变式探究：如图3，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，过点M作MG⊥x轴，过点N作NH⊥y轴，垂足分别为E、F、G、H． 试证明：EF ∥GH．
（本题10分）如图，在直角梯形ABCD中，AB∥CD，∠BCD=Rt∠，AB=AD=10cm，BC=8cm．点P从点A出发，以每秒3cm的速度沿折线ABCD方向运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动．已知动点P,Q同时出发，当点Q运动到点C时，P,Q运动停止，设运动时间为t．
（1）求CD的长；
（2）当四边形PBQD为平行四边形时，求四边形PBQD的周长；
（3）在点P,Q的运动过程中，是否存在某一时刻，使得△BPQ的面积为20cm2？若存在，请求出所有满足条件的t的值；若不存在，请说明理由．
（本题8分）某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元．为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．
（1）若商场平均每天要赢利1200元，且让顾客得到实惠，每件衬衫应降价多少元？
（2）要使商场平均每天赢利最多，则每件衬衫应降价多少元？
（本题8分）某校初三（1）班进行立定跳远训练，以下是李超和陈辉同学六次的训练成绩（单位：m）
| 1 |
2 |
3 |
4 |
5 |
6 |
|
| 李超 |
2．50 |
2．42 |
2．52 |
2．56 |
2．48 |
2．58 |
| 陈辉 |
2．54 |
2．48 |
2．50 |
2．48 |
2．54 |
2．52 |
（1）李超和陈辉的平均成绩分别是多少？
（2）分别计算两人的六次成绩的方差，哪个人的成绩更稳定？为什么？
（3）若预知参加级的比赛能跳过2．55米就可能得冠军，应选哪个同学参加？为什么？
（本题8分）在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．
（1）证明DE∥CB；
（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．
（本题6分）解一元二次方程: 