某商场推出优惠购买练习本和笔的促销活动，两种商品原售价分别为10元/本和3元/支。商场制定了两种优惠方案：（1）买一本练习本赠送1支笔；（2）按总价打8折。
（1）小赵需购买3本练习本和8支笔，选择哪种优惠方案合算？
（2）若某学校需购买300本练习本和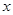
支笔（x≥300），试讨论选择哪种优惠方案更省钱？
某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，并且篮球的单价比足球的单价多20元，请解答下列问题：
（1）求出足球和篮球的单价；
（2）若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？
（3）在（2）的条件下，若已知足球的进价为50元，篮球的进价为65元，则在第二次购买方案中，哪种方案商家获利最多？
（1）已知方程x2＋px＋q＝0（p2－4q≥0）的两根为x1、x2，求证：x1＋x2＝－p，x1·x2＝q．
（2）已知抛物线y＝x2＋px＋q与x轴交于点A、B，且过点（―1，―1），设线段AB的长为d，当p为何值时，d2取得最小值并求出该最小值．
如图，点E、F分别是AD上的两点，AB∥CD，AB=CD，AF=DE．问：线段CE、BF有什么数量关系和位置关系？并加以证明．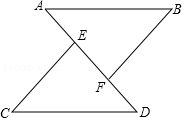
在平面直角坐标系xOy中，一次函数y＝－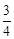
x＋3的图象与x轴交于点A，与y轴交于点B，动点P从点B出发沿BA向终点A运动，同时动点Q从点O出发沿OB向点B运动，到达点B后立刻以原来的速度沿BO返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点A时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t>0)秒．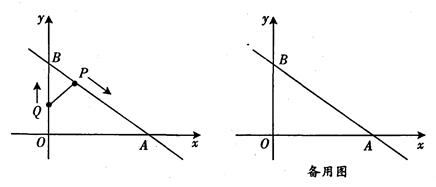
（1)求点P的坐标（用含t的代数式表示）；
（2)当点Q从点O向点B运动时（未到达点B)，是否存在实数t，使得△BPQ的面积大于17若存在，请求出t的取值范围；若不存在，请说明理由；
（3)伴随着P，Q两点的运动，线段PQ的垂直平分线为直线l．是否存在t的值，使得直线l经过点O?若存在，请求出所有t的值；若不存在，请说明理由．
化简：6a2b+2ab-3a2b2-7a-5ba-4b2a2-6a2b