等差数列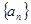 中,前三项分别为
中,前三项分别为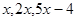 ,前
,前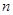 项和为
项和为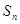 ,且
,且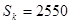 。
。
(1)、求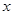 和
和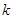 的值; (2)、求T=
的值; (2)、求T=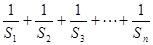
本题满分10分.
已知椭圆 ,椭圆上动点P的坐标为
,椭圆上动点P的坐标为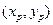 ,且
,且 为钝角,求
为钝角,求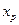 的取值范围。
的取值范围。
本题满分8分.
已知关于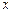 的实系数一元二次方程
的实系数一元二次方程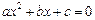 有两个虚数根
有两个虚数根 、
、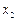 ,若
,若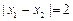 ,且
,且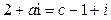 ,求方程的根
,求方程的根 、
、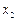 .
.
(本题满分13 分)
已知函数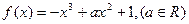
(1)若在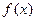 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若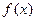 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数 的图象与函数
的图象与函数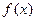 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
(本题满分13 分)
已知椭圆的右焦点F 与抛物线y2 =" 4x" 的焦点重合,短轴长为2.椭圆的右准线l与x轴交于E,过右焦点F 的直线与椭圆相交于A、B 两点,点C 在右准线l上,BC//x 轴.
(1)求椭圆的标准方程,并指出其离心率;
(2)求证:线段EF被直线AC 平分.
(本小题满分13 分)
如图(1)是一正方体的表面展开图,MN 和PB 是两条面对角线,请在图(2)的正方体中将MN 和PB 画出来,并就这个正方体解决下面问题。
(1)求证:MN//平面PBD;
(2)求证:AQ⊥平面PBD;
(3)求二面角P—DB—M 的大小.