如图所示,质量m=50kg的跳水运动员从距水面高h=10m的跳台上以v0=5m/s的速度斜向上起跳,最终落入水中。若忽略运动员的身高。取g=10m/s2,求: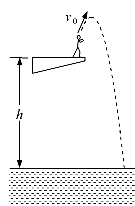
(1)运动员在跳台上时具有的重力势能(以水面为参考平面);
(2)运动员起跳时的动能;
(3)运动员入水时的速度大小。
从粒子源不断发射相同的带电粒子,初速度可忽略不计,这些粒子经电场加速后,从M孔以平行于MN方向进入一个边长为d的正方形的磁场区域MNQP,如图7所示,磁感应强度大小为B,方向垂直纸面向外,其中PQ的中点S开有小孔,外侧紧贴PQ放置一块荧光屏。当把加速电压调节为U时,这些粒子刚好经过孔S打在荧光屏上,不计粒子的重力和粒子间的相互作用。
(1)请说明粒子的电性
(2)求出粒子的比荷 。
。
如图所示,在空间中存在垂直纸面向外,宽度为d的有界匀强磁场。一质量为m、带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成30°角的方向垂直射入磁场,恰能垂直于上边界射出,不计粒子重力,题中d、m、q、v均为已知量。则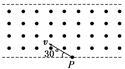
(1)粒子带何种电荷?
(2)磁场磁感应强度为多少?
短跑运动员完成100 m赛跑的过程可简化为匀加速运动和匀速运动两个阶段。一次比赛中,某运动员用11.00 s跑完全程。已知运动员在加速阶段的第2 s内通过的距离为7.5 m,求该运动员的加速度及在加速阶段通过的距离。
摩托车从A点由静止出发做匀加速直线运动,用7s时间通过一座长BC=14m的平桥,过桥后的速度是3m/s。求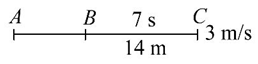
(1)它刚开上桥头时的速度vB有多大?
(2)桥头与出发点相距多远?
“嫦娥奔月”是中国人耳熟能详的美丽传说,“嫦娥工程”的顺利实施使这一传说就要变为现实。假如在月球上某航天员让一重物由静止开始自由下落,测出下落高度h=20m时,下落的时间正好为t=5s。则:
(1)月球表面的重力加速度g月为多大?
(2)重物下落2.5s时的瞬时速度为多大?