如图所示,某小型水电站发电机的输出功率为10kW,输出电压为400V,向距离较远的用户供电,为了减少电能损失,使用2kv高压输电,最后用户得到220V、9.5kW的电力,求:
(1)水电站升压变压器原、副线圈匝数比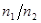
(2)输电线路导线电阻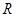 。
。
(3)用户降压变压器原、副线圈匝数比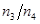 。
。
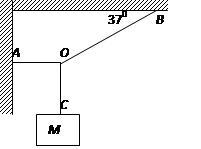
(6分)如图所示,质量为M=6kg的物体处于静止状态,细绳OB与水平方向夹角为37°,细绳OA沿水平方向。求:OA、OB两根细绳的拉力大小。(取g =" 10" m/s2,sin37°=0.6,cos37°=0.8)
 |
质量为5kg的木块放在水平木板上,木块与木板间的动摩擦因数为0.75,要使木块能沿木板匀速滑动,需给木块施加水平力为F,请画出木块在木板上匀速运动时的受力分析图,并求出力F的大小是多少?(g=10m/s2)
以10m/s的速度行驶的列车开始下坡,在坡路上做匀加速直线运动的加速度等于0.2m/s2,经来30s到达坡底,求:⑴列车到达坡底时的速度;⑵坡路的长度
如图所示,质量为m的小球通过轻绳悬挂在一倾角为θ的光滑斜面上,轻绳与斜面平行,开始时系统处于静止状态。
(1)求系统静止时,绳对小球的拉力大小和斜面对小球的支持力大小。
(2)当系统以多大的加速度向左运动时,斜面对小球的支持力恰好为零?
如图所示,有两根轻杆OA、OB,A、B两端可绕竖直墙上的光滑转轴转动,O点悬挂100N的重物,OB杆水平且与OA杆成夹角30°,求OA杆、OB杆在O点受到的力的大小。