已知：如图，梯形ABCD是等腰梯形，AB∥CD，AD=BC，AC⊥BC，BE⊥AB交AC的延长线于E，EF⊥AD交AD的延长线于F，下列结论：①BD∥EF；②∠AEF=2∠BAC；③AD=DF；④AC="CE+EF." 其中正确的结论有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（）
| A．0.845×104亿元 | B．8.45×103亿元 |
| C．8.45×104亿元 | D．84.5×102亿元 |
如图，从左面观察这个立体图形，能得到的平面图形是（）
A． |
B． |
C． |
D． |
的相反数是（）
| A．2 | B． |
C．﹣2 | D． |
如图，在平面直角坐标中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1，以A1B、BA为邻边作▱ABA1C1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1、B1A1为邻边作▱A1B1A2C2；…；按此作法继续下去，则Cn的坐标是（）
A．（﹣
×4n，4n） B．（﹣×4n﹣1，4n﹣1）
C．（﹣×4n﹣1，4n）D．（﹣×4n，4n﹣1）
如图，在正方形ABCD中，AC、BD相交于点O，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AG交BD于点F，连结EG、EF．下列结论：①tan∠AGB=2；②图中有9对全等三角形；③若将△GEF沿EF折叠，则点G不一定落在AC上；④BG=BF；⑤S四边形GFOE=S△AOF，上述结论中正确的个数是（）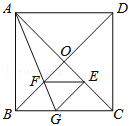
A．1个 B．2个 C．3个 D．4个