图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点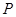 与点
与点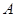 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点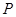 由
由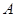 向
向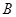 移动;当点
移动;当点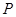 到过点
到过点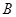 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有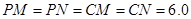 分米,
分米, 分米,
分米,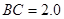 分米
分米
(1)求 长的取值范围; (2)当
长的取值范围; (2)当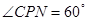 时,求
时,求 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为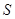 (结果保留
(结果保留 ).
).
已知:如图,在直角梯形ABCD中,AD // BC,AB⊥AD,BC = CD,BE⊥CD,垂足为点E,点F在BD上,联结AF、EF.
求证:AD = ED;
如果AF // CD,求证:四边形ADEF是菱形
某校为了解九年级500名学生平均每天课外阅读的时间,随机调查了该年级部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),现将有关数据整理后绘制成尚未完成的频率分布表和频数分布直方图:
| 组别 |
分组 |
频数 |
频率 |
| 1 |
14.5—24.5 |
7 |
0.14 |
| 2 |
24.5—34.5 |
a |
0.24 |
| 3 |
34.5—44.5 |
20 |
0. 4 |
| 4 |
44.5—54.5 |
6 |
b |
| 5 |
54.5—64.5 |
5 |
0.1 |

被调查的学生有名
频率分布表中,a= ,b=
补全频数分布直方图;
被调查学生一周内平均每天课外阅读时间的中位数落在组;
请估计该年级学生中,大约有名学生平均每天课外阅读的时间不少于35分钟.
一商店1月份的利润是2500元,3月份的利润达到3025元,这两个月的利润平均月增长的百分率是多少?
解方程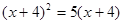
2x2―3x―5=0

先化简,再求值: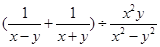 ,其中
,其中 