若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律:
根据以上规律,回答以下问题:商高数的三个数中,有几个偶数,几个奇数?
写出各数都大于30的两组商高数。
用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
理解同解方程的定义,再解题:
(1)同解方程的定义为:如果两个方程的解相同,那么这两个方程叫同解方程;反之如果两个方程是同解方程,那么这两个方程的解是一样的;例如x+1=4与x+51=54的解都是x=3,这两个方程是同解方程;(2)已知方程4x-a=1与方程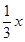 +(a+2)=3x+2都是关于x的方程,且这两个方程的解相同,求它们的解。
+(a+2)=3x+2都是关于x的方程,且这两个方程的解相同,求它们的解。
右图的数阵是由一些奇数排成的. 1 3 5 7 9
(1)右图框中的四个数有什么关系? 11 13  15 17 19
15 17 19
(设框中第一行第一个数为 )………………
)………………
(2)若这样框出的四个数的和是200,求这四个数. 91 93 95 97 99
(3)是否存在这样的四个数,它们的和为420,为什么?
甲、乙两人骑自行车,同 时从相距65千米的两地相向而行,甲的速度是17.5千米/时,乙的速度为15千米/时,经过几小时,两人相距32.5千米?
时从相距65千米的两地相向而行,甲的速度是17.5千米/时,乙的速度为15千米/时,经过几小时,两人相距32.5千米?
展开你想象的翅膀,尽可能多地从方程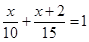 中猜想出它可能会是哪种类型的实际问题,将其编写出来,并解答之.
中猜想出它可能会是哪种类型的实际问题,将其编写出来,并解答之.
如果方程 的解与方程
的解与方程 的解相同,求式子
的解相同,求式子 的值 .
的值 .