在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N .写出点C的坐标;
求证:MD = MN;
连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明.

已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.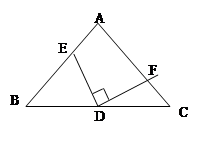
如果∠A=90°求证:DE=DF
如果DF//AB,则结论:“四边形AEDF为直角梯形”是否正确,若正确,请证明;若不正确,请画出草图举反例
已知:如图,正比例函数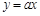 的图象与反比例函数
的图象与反比例函数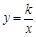 的图象交于点
的图象交于点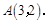
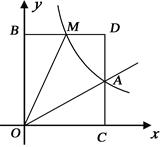
试确定上述正比例函数和反比例函数的表达式;
根据图象直接回答,在第一象限内,当
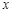 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?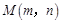 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中 ,过点
,过点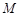 作直线
作直线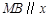 轴,交
轴,交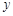 轴于点
轴于点 ;过点
;过点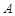 作直线
作直线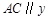 轴交
轴交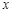 轴于点
轴于点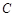 ,交直线
,交直线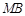 于点
于点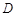 .当四边形
.当四边形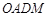 的面积为6时,请判断线段
的面积为6时,请判断线段 与
与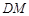 的大小关系,并说明理由.
的大小关系,并说明理由.
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.判断DE与⊙O的位置关系,并证明你的结论
若DE的长为2
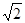 ,cosB=,求⊙O的半径.
,cosB=,求⊙O的半径.
使得函数值为零的自变量的值称为函数的零点.例如,对于函数 ,令
,令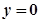 ,可得
,可得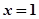 ,我们就说
,我们就说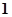 是函数
是函数 的零点.请根据零点的定义解决下列问题:已知函数
的零点.请根据零点的定义解决下列问题:已知函数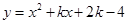 (k为常数).当k=2时,求该函数的零点;
(k为常数).当k=2时,求该函数的零点;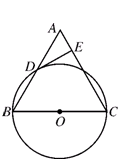
两幢垂直于地面的大楼相距110米,从甲楼顶部看乙楼顶部的仰角为30°,已知甲楼高35米根据题意,在图中画出示意图;
求乙楼的高度为多少米?