阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
 的有理化因式是 .
的有理化因式是 .  分母有理化得 .
分母有理化得 .
分母有理化:(1)
 ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)"  =______..
=______..
计算:
 .
.
如图所示,已知在直角梯形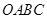 中,
中,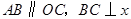 轴于点
轴于点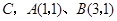 .动点
.动点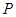 从
从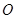 点出发,沿
点出发,沿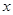 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过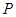 点作
点作 垂直于直线
垂直于直线 ,垂足为
,垂足为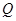 .设
.设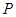 点移动的时间为
点移动的时间为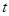 秒(
秒(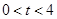 ),
),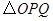 与直角梯形
与直角梯形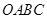 重叠部分的面积为
重叠部分的面积为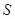 .
.求经过
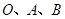 三点的抛物线解析式;
三点的抛物线解析式;将
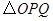 绕着点
绕着点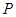 顺时针旋转
顺时针旋转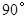 ,是否存在
,是否存在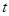 ,使得
,使得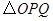 的顶点
的顶点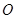 或
或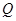 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出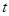 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.求
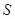 与
与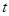 的函数关系式.
的函数关系式.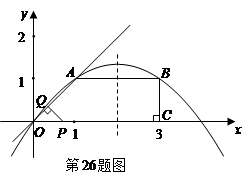
如图,在直角坐标系中,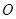 是原点,
是原点, 三点的坐标分别
三点的坐标分别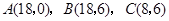 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿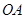 向终点
向终点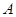 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点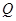 沿
沿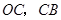 向终点
向终点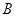 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.求直线
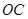 的解析式.
的解析式.设从出发起,运动了
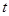 秒.如果点
秒.如果点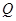 的速度为每秒
的速度为每秒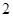 个单位,试写出点
个单位,试写出点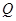 的坐标,并写出此时
的坐标,并写出此时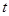 的取值范围.
的取值范围.设从出发起,运动了
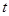 秒.当
秒.当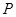 ,
,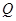 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形 的周长的一半,这时,直线
的周长的一半,这时,直线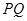 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出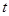 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.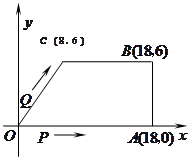
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.求证:∠DAF=∠CDE
问△ADF与△DEC相似吗?为什么?
若AB=4,AD=3
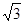 ,AE=3,求AF的长.
,AE=3,求AF的长.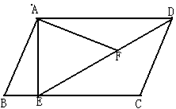
为了拉动内需,我省启动“家电下乡”活动。在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.A型洗衣机和B型洗衣机的售价各是多少元?
小李和小王购买洗衣机除财政补贴外实际各付款多少元?
在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).小明的这三件文具中,可以看做是轴对称图形的是___________(填字母代号);
小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?