问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题:
① 如图1,O是正三角形ABC的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 120°,则四边形OPBQ的面积等于三角形ABC面积的三分之一.
② 如图2,O是正方形ABCD的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 90°,则四边形OPBQ的面积等于正方形ABCD面积的四分之一.然后运用类比的思想提出了如下的命题:
③ 如图3,O是正五边形ABCDE的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 72°,则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
、任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(2)请你继续完成下面的探索:
如图④,在正n(n≥3)边形ABCDEF…中,O是中心,∠MON分别与AB、BC交于点P,Q,若∠MON等于多少度时,则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一?(不要求证明)
解:(1)我选 .
证明: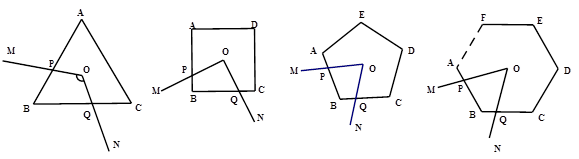
如图,已知在△ 中,∠A=∠B
中,∠A=∠B 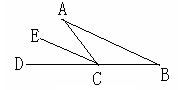
(1)请你添加一个与直线AB有关的条件,由此可推得CE是∠ACD的角平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的角平分线. (要写出理由)
根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如下(部分信息未给出):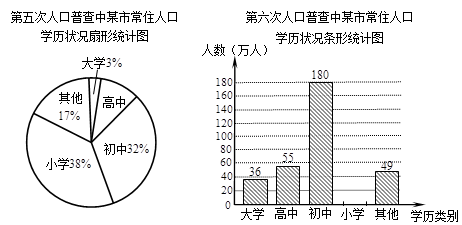
解答下列问题:
(1)计算第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)第六次人口普查结果与第五次相比,该市常住人口中高中学历人数增长的百分比是多少?
有这样一道题:“当 =0.302,
=0.302, =-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“
=-0.239时,求(a+b)(a-b)+(4ab-8a2b2)÷4ab-a(a-2 b)多项式的值”,有一位同学指出题目中所给的条件“ =0.302,
=0.302, =-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
=-0.239”是多余的,问这位同学说的是否正确?若正确,请说明其理由;若不正确,多项式的值该是多少?
在同一副扑克中抽出了16张牌,其中红心有x张,方块有2x张,其他均为梅花,现将这16张牌洗匀背面朝下放在桌面上,A同学任意抽1张,若为红心则A同学获胜,A同学把抽出的牌放回并洗匀背面朝下放在桌面上,B同学再任意抽1张,若为梅花,则B同学获胜.
(1)当X=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
(1)在图①正方形网格中,已知∠AOB及点E、F,现要求只用直尺,分别以E、F为顶点.画∠CEH、∠PFK,使∠CEH与∠AOB互余,且CE与OB互相垂直;使∠PFK与∠AOB互补,且FP∥OA,FK∥OB.
(2)在图②中,已知∠AOB,点E在OB上,请先用量角器画射线EC,使EC⊥EB于E,交OA于C,再用尺规作射线EH,使∠CEH与∠AOB互余,且EH∥OA.
(保留痕迹,不写作或画法,不说明理由).