某超市销售一种新鲜“酸奶”， 此“酸奶”以每瓶3元购进，5元售出.这种“酸奶”的保质期不超过一天，对当天未售出的“酸奶”必须全部做销毁处理.
（1）该超市某一天购进20瓶酸奶进行销售.若设售出酸奶的瓶数为x（瓶），销售酸奶的利润为y（元），写出这一天销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式.为确保超市在销售这20瓶酸奶时不亏本，当天至少应售出多少瓶？
（2）小明在社会调查活动中，了解到近10天当中，该超市每天购进酸奶20瓶的销售情况统计如下：
| 每天售出瓶数 |
17 |
18 |
19 |
20 |
| 频数 |
1 |
2 |
2 |
5 |
根据上表，求该超市这10天每天销售酸奶的利润的平均数；
（3）小明根据（2）中，10天酸奶的销售情况统计，计算得出在近10天当中，其实每天购进19瓶总获利要比每天购进20瓶总获利还多.你认为小明的说法有道理吗？试通过计算说明.
（本小题７分）抛物线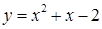
交
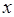轴于点A、B，交
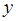轴于点C，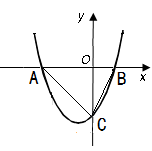
（1）求出抛物线的对称轴及顶点坐标；
（2）根据图象回答：当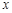
取何值时，
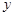＜0；
（3）求△ABC的面积．
（本小题6分）已知关于x的一元二次方程mx2+nx+1=0有两个相等的实数根，求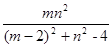
的值。
为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室．经预算，一共需要筹资30000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊．
（1）筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？
（2）经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户共集资20000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a%（其中a＞0）．则每户平均集资的资金在150元的基础上减少了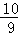
a%，求a的值．
某汽车专卖店销售A，B两种型号的新能源汽车，上周售出1辆A型车和3辆B型车，销售额为96万元，本周已售出2辆A型车和1辆B型车，销售额为62万元。
（1）求每辆A型车和B型车的售价各多少万元。
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元，则有哪几种购车方案？
．甲、乙两人准备整理一批新到的图书，甲单独整理需要40分钟完工；若甲、乙共同整理20分钟后，乙需再单独整理30分钟才能完工．问乙单独整理这批图书需要多少分钟完工？