先阅读下面材料，再解答问题：
初中数学教科书中有这样一段叙述：“要比较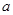
与
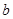的大小，可先求出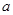与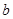的差，再看这个差是正数，负数还是零.由此可见，要比较两个代数式值的大小，只要考虑它们的差就可以了.
甲、乙两人两次同时在同一粮店购买粮食（假设两次购买粮食的单价不相同），甲每次购买粮食100千克，乙每次购买粮食用去100元，设甲、乙两人第一次购粮食的单价为每千克x元，第二次购买粮食的单价为每千克y元
（1）用含x、y的代数式表示：甲每次购买粮食共需要付款______元，乙两次共购买_________千克粮食，若甲两次购买粮食的平均单价为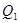
元，乙两次购买粮食的平均单价为
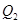元，
则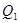=_______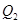，=_________. (共四个填空）
（2）若规定“谁两次购买粮食的平均单价低，谁的购买粮食方式更合算”，请你判断甲、乙两人的购买粮食方式那一个更合算些，并说明理由.
如图，身高1.6米的小明从距路灯的底部（点O）20米的点A沿AO方向行走14米到点C处,小明在A处，头顶B在路灯投影下形成的影子在M处。
（1）已知灯杆垂直于路面，试标出路灯P的位置和小明在C处，头顶D在路灯投影下形成的影子N的位置。
（2）若路灯（点P）距地面8米，小明从A到C时，身影的长度是变长了还是变短了？变长或变短了多少米？
如图，请在下列三个关系中，选出两个恰当的关系作为条件，填在已知条件的横线上，推出四边形ABCD是平行四边形，并予以证明。
关系：①AD∥BC，②AB＝CD，③∠A＝∠C。
已知：在四边形ABCD中，，．
求证：四边形ABCD是平行四边形．
，当y＝－1时，再从－2＜x＜3的范围内选取一个合适的整数x代入求值.
．
解不等式组：
，并把它的解集表示在数轴上．