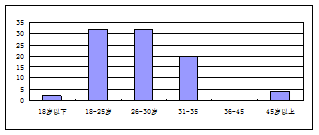
某联通公司对重庆市部分市民使用苹果iphone产品的年龄分布情况进行了统计,制成了如下两幅不完整的统计图:
|
|
|
|
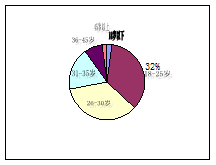
|
(本题满分8分,每小题4分)解方程:
(1)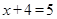
(2)已知方程 是关于x 的一元一次方程.求m的值并解这个一元一次方程.
是关于x 的一元一次方程.求m的值并解这个一元一次方程.
(本题满分6分,其中每问3分)如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
(1)若线段DE=10cm,求线段AB的长.
(2)若线段CE=8cm,求线段DB的长.
(本题满分6分,每小题3分)
(1)计算:
(2)已知A=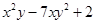 ,B=
,B=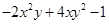 ,求2A+B.
,求2A+B.
小王玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去。
(1)填空:当小王撕了3次后,共有张纸片;
(2)填空:当小王撕了n次后,共有张纸片.(用含n的代数式表示)
(3)小王说:我撕了若干次后,共有纸片2013张,小王说的对不对?若不对,请说明你的理由;若对的,请指出小王需撕多少次?
出租车司机小李某天下午的营运全是在东西走向的城中路上进行的,如果规定向东行驶为正,他这天下午行车的里程(单位:千米)如下:
+8, -7, +10, -6, +3, -5, +9, -6
(1)小李下午出发地记为0,他将最后一名乘客送抵目的地时,小李在出发地的什么方向?距下午出发地有多远?
(2)如果汽车耗油量为0.5升/千米,油箱容量为26升,若出发时油箱装满汽油,请你判断途中是否需要补充汽油?