平面内两条直线 ∥
∥ ,它们之间的距离等于
,它们之间的距离等于 .一块正方形纸板
.一块正方形纸板 的边长也等
的边长也等
于 .现将这块硬纸板如图所示放在两条平行线上.
.现将这块硬纸板如图所示放在两条平行线上.如图1,将点C放置在直线
 上, 且
上, 且 于O, 使得直线
于O, 使得直线 与
与 、
、 相交于E、F,证明:
相交于E、F,证明: 的周长等于
的周长等于 ;
;请你继续完成下面的探索:如图2,若绕点C转动正方形硬纸板
 ,使得直线
,使得直线 与
与 、
、 相交于E、F,
相交于E、F,
试问 的周长等于
的周长等于 还成立吗?并证明你的结论;
还成立吗?并证明你的结论;如图3,将正方形硬纸片
 任意放置,使得直线
任意放置,使得直线 与
与 、
、 相交于E、F,直线
相交于E、F,直线 与
与 、CD相交于G,H,设
、CD相交于G,H,设 AEF的周长为
AEF的周长为 ,
, CGH的周长为
CGH的周长为 ,试问
,试问
 ,
, 和
和 之间存在着什么关系?试证明你的结论.
之间存在着什么关系?试证明你的结论.


经过原点和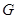 (4,0)的两条抛物线
(4,0)的两条抛物线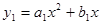 ,
,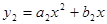 ,顶点分别为
,顶点分别为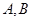 ,且都在第1象限,连结
,且都在第1象限,连结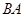 交
交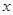 轴于
轴于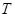 ,且
,且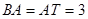 .
.分别求出抛物线
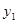 和
和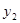 的解析式;
的解析式;点C是抛物线
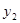 的
的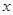 轴上方的一动点,作
轴上方的一动点,作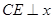 轴于
轴于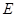 ,交抛物线
,交抛物线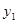 于D,试判断
于D,试判断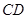 和
和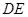 的数量关系,并说明理由;
的数量关系,并说明理由;直线
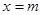 ,交抛物线
,交抛物线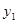 于M,交抛物线
于M,交抛物线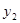 于N,是否存在以点
于N,是否存在以点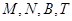 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出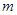 的值;若不存在,说明理由..
的值;若不存在,说明理由..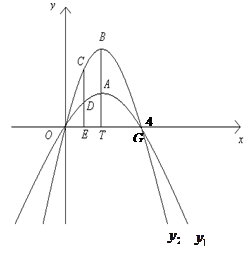
已知直线 于O,现将矩形ABCD和矩形EFGH,如图1放置,直线BE分别交直线
于O,现将矩形ABCD和矩形EFGH,如图1放置,直线BE分别交直线 于
于 .
.
当矩形ABCD≌矩形EFGH时,(如图1) BM与 NE的数量关系是;
当矩形ABCD与矩形EFGH不全等,但面积相等时,把两矩形如图2,3那样放置,问在这两种放置的情形中,(1)的结论都还成立吗?如果你认为都成立,请你利用图3给予证明,若认为BM与 NE的有不同的数量关系,先分别写出其数量关系式,再证明.
如图, ⊙O的半径为4㎝, 是⊙O的直径,
是⊙O的直径, 切⊙O于点
切⊙O于点 ,且
,且 =4㎝,当点P在⊙O上运动时,是否存在点P,使得△
=4㎝,当点P在⊙O上运动时,是否存在点P,使得△ 为等腰三角形,若存在,有几个符合条件的点
为等腰三角形,若存在,有几个符合条件的点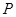 ,并分别求出点
,并分别求出点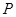 到线段
到线段 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
一张长方形桌子有6个座位.按甲方式将桌子拼在一起.

3张桌子拼在一起共有个座位,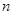 张桌子拼在一起共有个座位;
张桌子拼在一起共有个座位;按乙方式将桌子拼在一起.

3张桌子拼在一起共有个座位,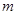 张桌子拼在一起共有个座位;
张桌子拼在一起共有个座位;某食堂有A,B两个餐厅,现有200张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将
 张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有790个座位,问A,B两个餐厅各有多少个座位?
张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有790个座位,问A,B两个餐厅各有多少个座位?