设函数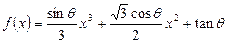 ,其中
,其中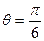 ,则导数
,则导数 的值是( )
的值是( )
| A.2 | B. |
C.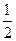 |
D. |
在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的
概率是()
A. |
B.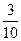 |
C. |
D. |
设 的三个内角为A,B,C,向量
的三个内角为A,B,C,向量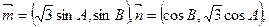 若
若 ,则C=()
,则C=()
A. |
B.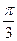 |
C.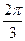 |
D. |
我国的《洛书》中记载着世界上最古老的一个幻方:
将1,2,…,9填入3×3的方格内,使三行、三列、
二对角线的三个数之和都等于15,如图1所示,一
般地,将连续的正整数1,2,3,…n2填入n×n个
方格中,使得每行、每列、每条对角线上的数的和
相等,这个正方形就叫做n阶幻方,记n阶幻方的
对角线上数的和为N,如图1的幻方记为N3=15,
那么N12的值为()
| A.869 | B.870 | C.871 | D.875 |
已知圆 对称,则ab的取值范围是()
对称,则ab的取值范围是()
A.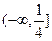 |
B.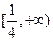 |
C.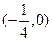 |
D.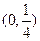 |