(本小题满分12分)
已知椭圆C: 的离心率为
的离心率为 ,且过点Q(1,
,且过点Q(1, ).
).
(1) 求椭圆C的方程;
(2) 若过点M(2,0)的直线与椭圆C相交于A,B两点,设P点在直线
上,且满足 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值.
.(本小题满分12分)
为了解某校高三学生质检数学成绩分布,从该校参加质检的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图.若第一组至第五组数据的频率之比为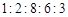 ,最后一组数据的频数是6.
,最后一组数据的频数是6.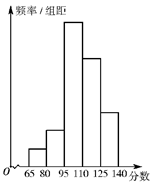
(Ⅰ)估计该校高三学生质检数学成绩在125~140分之间的概率,并求出样本容量;
(Ⅱ)从样本中成绩在65~95分之间的学生中任选两人,求至少有一人成绩在65~80分之间的概率.
已知定义在R上的函数 ,其中a、b为常数。
,其中a、b为常数。
(1)若曲线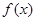 在点
在点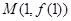 处的切线方程为
处的切线方程为 ,求a、b的值;
,求a、b的值;
(2)若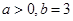 ,且函数
,且函数 在
在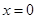 处取得最大值,求实数a的取值范围。
处取得最大值,求实数a的取值范围。
已知椭圆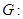
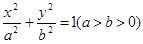 的离心率为
的离心率为 =
= ,椭圆
,椭圆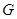 上的点
上的点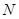 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆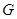 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点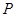 在椭圆上,且位于
在椭圆上,且位于 轴的上方,
轴的上方, .
.
(I)求椭圆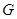 的方程;
的方程;
(II)求点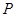 的坐标;
的坐标;
(III)设 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点, 到直线AP的距离等于
到直线AP的距离等于 ,求椭圆上的点到点
,求椭圆上的点到点 的距离
的距离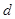 的最小值.
的最小值.
如图,在底面是矩形的四棱锥P—ABCD中, 面ABCD,E是PD的中点。
面ABCD,E是PD的中点。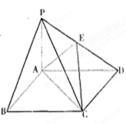
(1)求证:平面 平面PDA;
平面PDA;
(2)求几何体P—ABCD被平面ACE分得的两部分的体积比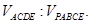
已知数列 中,
中, ,且满足
,且满足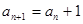 ,
,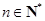 .
.
(I)求数列 的通项公式;
的通项公式;
(II)设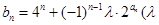 为非零整数,
为非零整数,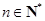 ),试确定
),试确定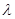 的值,使得对任意
的值,使得对任意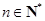 ,都有
,都有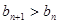 成立.
成立.